Introduzione all'elaborazione dei segnali: filtro a media mobile

Segnali e sistemi sono concetti centrali nell'ingegneria elettrica, che ci permettono di modellare il modo in cui le informazioni passano attraverso i componenti elettrici e vengono modificate. Inoltre, una volta compreso il modo in cui segnali come la tensione sono influenzati da diversi componenti elettrici, possiamo progettare circuiti per manipolare i segnali come vogliamo. È interessante come si possa utilizzare una combinazione di componenti elettrici - resistori, condensatori e amplificatori operazionali - per modellare strumenti matematici quali l'integrazione e la differenziazione.

Ad esempio, diamo un'occhiata al seguente circuito (Figura 1):

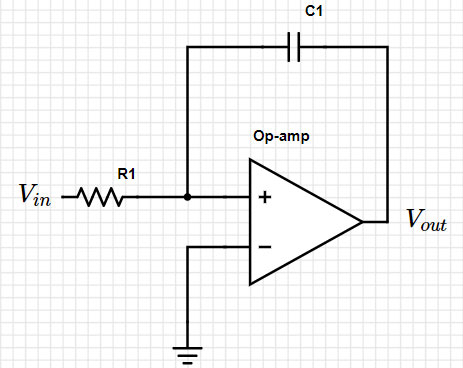Figura 1: Semplice circuito integratore. (Immagine per gentile concessione di Mustahsin Zarif)

Passando al dominio di Laplace, possiamo rappresentare il circuito con la formula:

Vout = -(1/s) (1/RC) Vin

1/s nel dominio di Laplace corrisponde in realtà all'integrazione! Abbiamo quindi un modello per un circuito integratore che utilizza un amplificatore operazionale. Tuttavia, quando guardiamo il mondo reale, i sistemi sono sempre soggetti a una qualche forma di rumore casuale.

Mettendo da parte il circuito integratore per un esempio più semplice, consideriamo un circuito amplificatore di tensione le cui forme d'onda di ingresso e di uscita possono essere misurate con un oscilloscopio, come illustra la Figura 2.

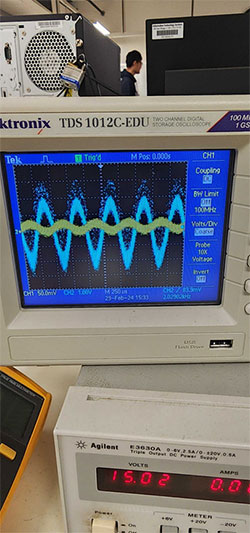Figura 2: Forme d'onda di ingresso e uscita dell'amplificatore di tensione. (Immagine per gentile concessione di Mustahsin Zarif)

Il rumore casuale che si aggiunge alle forme d'onda sinusoidali visibili sottostanti può essere dovuto a una moltitudine di fattori, ad esempio da collegamenti elettrici scadenti poiché il circuito è costruito su una basetta sperimentale. Questo rumore incide anche sulla forma d'onda dell'integratore, come vedremo in un prossimo blog di questa serie sull'elaborazione del segnale. Tuttavia, ciò che spesso ci interessa è come ridurre al minimo i disturbi casuali.

Tecniche di filtraggio

Gli ingegneri cercano di superare questi ostacoli utilizzando tecniche di filtraggio, che possono essere classificate come 1) filtri a risposta impulsiva finita (FIR) o 2) filtri a risposta impulsiva infinita (IIR).

I filtri FIR sono così chiamati perché l'uscita in ogni momento dipende solo dai valori attuali e precedenti dell'ingresso e non dai valori passati dell'uscita. Pertanto, ha una struttura non ricorsiva senza retroazione che può essere modellata come Equazione 1.

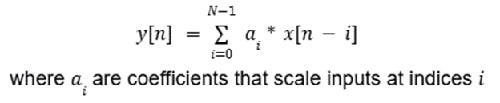Equazione 1: Esempio di equazione del filtro FIR. (Immagine per gentile concessione di Mustahsin Zarif)

Il circuito integratore è un esempio di filtro FIR, perché l'uscita dipende solo dall'ingresso.

I filtri IIR invece hanno una retroazione, poiché l'uscita in ogni momento dipende dalle uscite precedenti e dall'ingresso corrente. Questo comportamento è modellato come Equazione 2.

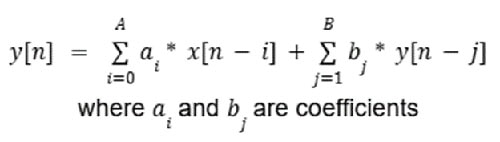Equazione 2: Esempio di equazione del filtro IIR. (Immagine per gentile concessione di Mustahsin Zarif)

La figura 3 è la rappresentazione visiva del diagramma a blocchi di un filtro IIR, che mostra come gli ingressi e le uscite vengono ritardati (z-i, z-j), ridimensionati (ai, bj) e sommati per ottenere l'uscita attuale. Modificando questi valori possiamo implementare diversi tipi di filtri.

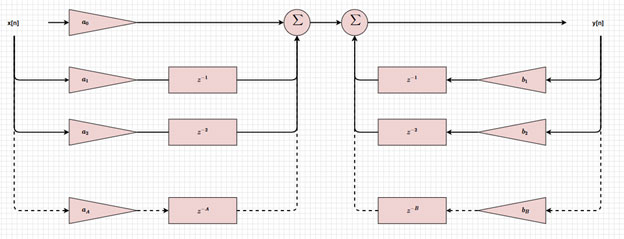Figura 3: Diagramma a blocchi di un filtro IIR. (Immagine per gentile concessione di Mustahsin Zarif)

Se volessimo il diagramma a blocchi di un filtro FIR senza retroazione, y[n] sarebbe semplicemente il risultato della prima sommatoria (Figura 4).

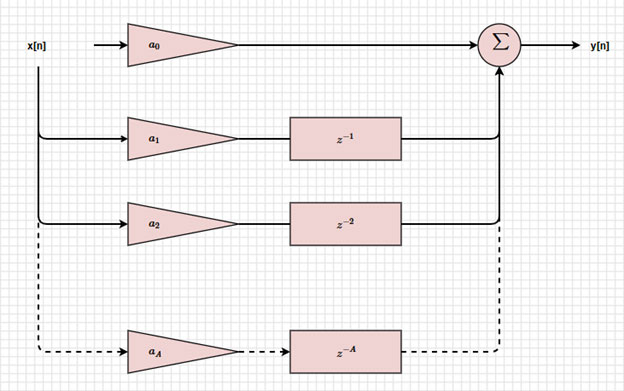Figura 4: Diagramma a blocchi di un filtro FIR. (Immagine per gentile concessione di Mustahsin Zarif)

Ora che abbiamo capito le basi dei filtri FIR e IIR, usiamo un esempio per illustrare quanto appreso: il filtro a media mobile.

La media mobile funziona calcolando la media tra l'ingresso corrente e un certo numero di ingressi precedenti (equazione 3).

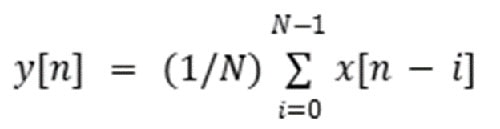Equazione 3: Equazione della media mobile. (Immagine per gentile concessione di Mustahsin Zarif)

Dove N = dimensione della finestra/numero di campioni che contribuiscono all'uscita

Possiamo vedere che si tratta di un filtro FIR, poiché non ci sono termini y sul lato destro dell'equazione.

Tuttavia, possiamo riorganizzare l'equazione per formare un filtro IIR. Si consideri l'esempio seguente:

Sia N=5, quindi

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5,

e y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

Pertanto, l'uscita corrente ora dipende dall'uscita precedente (y[6] dipende da y[5])!

In termini generali,

y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N

Dove N = dimensione della finestra

Questo filtro fa miracoli nel livellare i segnali nel dominio temporale, come mostra la Figura 5 che ho simulato utilizzando Python per una dimensione della finestra N = 11.

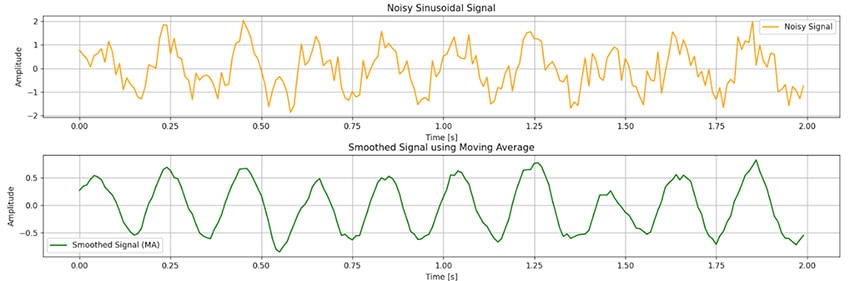Figura 5: Simulazione di un filtro mobile in Python. (Immagine per gentile concessione di Mustahsin Zarif)

Codice Python per la simulazione del filtro mobile:

Copyimport numpy as np

import matplotlib.pyplot as plt



# Parameters for the sinusoidal wave

frequency = 5  # in Hertz

sampling_rate = 100  # Sampling rate in samples per second

duration = 2  # in seconds



# Generate time axis

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# Generate a clean sinusoidal signal

clean_signal = np.sin(2  np.pi  frequency * t)



# Add random, white (Gaussian) noise to the signal

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

    window = np.ones(window_size) / window_size

    return np.convolve(signal, window, mode='same') 



# Apply moving average to the noisy signal

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# Plot the noisy and smoothed signals

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

Conclusione

Abbiamo iniziato questo blog mostrando come, nel mondo reale, i dati siano inficiati dal rumore. Sebbene non sia possibile ottenere la risposta ideale che ci aspetteremmo da equazioni matematiche, è possibile filtrare le caratteristiche indesiderate dai dati raccolti per far sì che corrispondano il più possibile alla risposta ideale. Esistono diversi metodi per farlo e vari scenari in cui dovremmo farlo. Questo blog si conclude con una risposta simulata del filtro a media mobile. Nel prossimo blog guarderemo a un filtro a media mobile esponenziale per capire come livellare i dati rumorosi di un'unità di misurazione inerziale(IMU).