Elaborazione dei segnali: filtro di media mobile esponenziale (EMA)

Nel precedente blog Introduzione all'elaborazione dei segnali avevamo visto le due classi di filtri: risposta impulsiva finita (FIR) e risposta impulsiva infinita (IIR). Avevamo visto come il filtro di media mobile può essere espresso sia in forma FIR che IIR. Quali sono i vantaggi dell'uno rispetto all'altro?

Ripensando all'esempio del mio blog precedente, il filtro FIR espanso ha la forma:

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1]+x[0])/5,

Vediamo che servono:

1. 5 moltiplicazioni e
2. 4 addizioni.

Le operazioni di moltiplicazione sono particolarmente costose dal punto di vista computazionale pertanto, se osserviamo nuovamente il modulo IIR, vediamo che richiede solo:

1. 3 moltiplicazioni e
2. 2 addizioni

y[6]=(x[6]+y[5]-x[1])/5

Ciò riduce notevolmente i costi in termini di calcolo! Questo è un vantaggio per i dispositivi embedded come i microcontroller, poiché impiegano meno risorse in ogni fase temporale discreta per eseguire i calcoli.

Ad esempio, se utilizzo la funzione Python 'time.time' per il filtro di media mobile a 11 punti in formato FIR e IIR, con tutti i parametri (dimensione della finestra, frequenza di campionamento, dimensione del campione, ecc.) uguali, ottengo rispettivamente i seguenti risultati di runtime: 51 ms, 27 ms.

Esempio di filtro IIR a tempo discreto

Ora che abbiamo intuito perché i filtri IIR sono migliori per i microcontroller, guardiamo un progetto di esempio con Arduino UNO e una IMU (unità di misurazione inerziale) MPU6050 di DFRobot (Figura 1). Applicheremo il filtro della media mobile esponenziale (EMA) ai dati IMU per vedere le differenze tra i dati grezzi e quelli livellati.

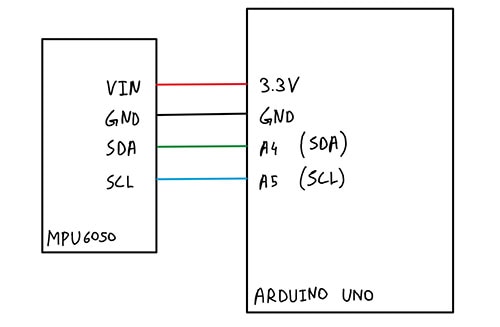Figura 1: Diagramma a blocchi del collegamento tra MPU6050 e Arduino Uno. (Immagine per gentile concessione di Mustahsin Zarif)

Figura 2: Connessione tra MPU6050 e Arduino Uno. (Immagine per gentile concessione di Mustahsin Zarif)

Il filtro di media mobile esponenziale è di forma ricorsiva:

y[n] = α*x[n] + (1- α)*y[n-1]

È ricorsivo perché ogni output attuale misurato dipende anche dagli output precedenti, nel senso che il sistema ha memoria.

La costante alpha() determina quanto peso vogliamo dare all'input attuale rispetto agli output precedenti. Per chiarezza, espandiamo l'equazione per ottenere:

y[n] = α*x[n] + (1- α )*(α*x[n−1]+(1−α)*y[n−2])

y[n] = α*x[n] + (1- α )*x[n−1]+α*(1−α)2*x[n−2])+ ...

y[n] = k=0nα*(1−α)k*x[n−k]

Osserviamo che maggiore è alpha, più l'input attuale influenza l'output attuale. Questo fatto è positivo perché, se il sistema è in evoluzione, i valori molto nel passato non sono rappresentativi del sistema attuale. Per contro, ciò sarebbe negativo se, ad esempio, si verificasse un cambiamento improvviso e momentaneo nel sistema rispetto alla normalità; in questo caso, vorremmo che il nostro output seguisse la tendenza degli output precedenti.

Ora vediamo come funzionerebbe il codice per un filtro EMA per MPU6050.

Codice filtro EMA:

Copy#include <wire.h>
#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];
float accelYBuffer[BUFFER_SIZE];
float accelZBuffer[BUFFER_SIZE];
int bufferCount = 0;  

void setup() {
  Serial.begin(115200);
  Wire.begin();

  mpu.initialize();

  if (!mpu.testConnection()) {
    Serial.println("MPU6050 connection failed!");
    while (1);
  }

  int16_t ax, ay, az;
  for (int i = 0; i < BUFFER_SIZE; i++) {
    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);
    accelXBuffer[i] = ax / 16384.0;
    accelYBuffer[i] = ay / 16384.0;
    accelZBuffer[i] = az / 16384.0;
  }
  bufferCount = BUFFER_SIZE;
}

void loop() {
  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;
  float accelY_float = accelY / 16384.0;
  float accelZ_float = accelZ / 16384.0;

  if (bufferCount < BUFFER_SIZE) {
    accelXBuffer[bufferCount] = accelX_float;
    accelYBuffer[bufferCount] = accelY_float;
    accelZBuffer[bufferCount] = accelZ_float;
    bufferCount++;
  } else {
    for (int i = 1; i < BUFFER_SIZE; i++) {
      accelXBuffer[i - 1] = accelXBuffer[i];
      accelYBuffer[i - 1] = accelYBuffer[i];
      accelZBuffer[i - 1] = accelZBuffer[i];
    }
    accelXBuffer[BUFFER_SIZE - 1] = accelX_float;
    accelYBuffer[BUFFER_SIZE - 1] = accelY_float;
    accelZBuffer[BUFFER_SIZE - 1] = accelZ_float;
  }

//calculate EMA using acceleration values stored in buffer
  float emaAccelX = accelXBuffer[0];
  float emaAccelY = accelYBuffer[0];
  float emaAccelZ = accelZBuffer[0];
  float alpha = 0.2;

  for (int i = 1; i < bufferCount; i++) {
    emaAccelX = alpha * accelXBuffer[i] + (1 - alpha) * emaAccelX;
    emaAccelY = alpha * accelYBuffer[i] + (1 - alpha) * emaAccelY;
    emaAccelZ = alpha * accelZBuffer[i] + (1 - alpha) * emaAccelZ;
  }

  Serial.print(accelX_float); Serial.print(",");
  Serial.print(accelY_float); Serial.print(",");
  Serial.print(accelZ_float); Serial.print(",");
  Serial.print(emaAccelX); Serial.print(",");
  Serial.print(emaAccelY); Serial.print(",");
  Serial.println(emaAccelZ);

  delay(100);
}
</mpu6050.h></wire.h>

Quando eseguiamo questo codice e controlliamo il plotter seriale, possiamo vedere linee grezze e livellate a coppie per le accelerazioni sugli assi X, Y e Z, utilizzando una dimensione della finestra di 11 e un valore alpha di 0,2 (Figure da 3 a 5).

Figura 3: Valori di accelerazione grezzi e filtrati nella direzione X. (Immagine per gentile concessione di Mustahsin Zarif)

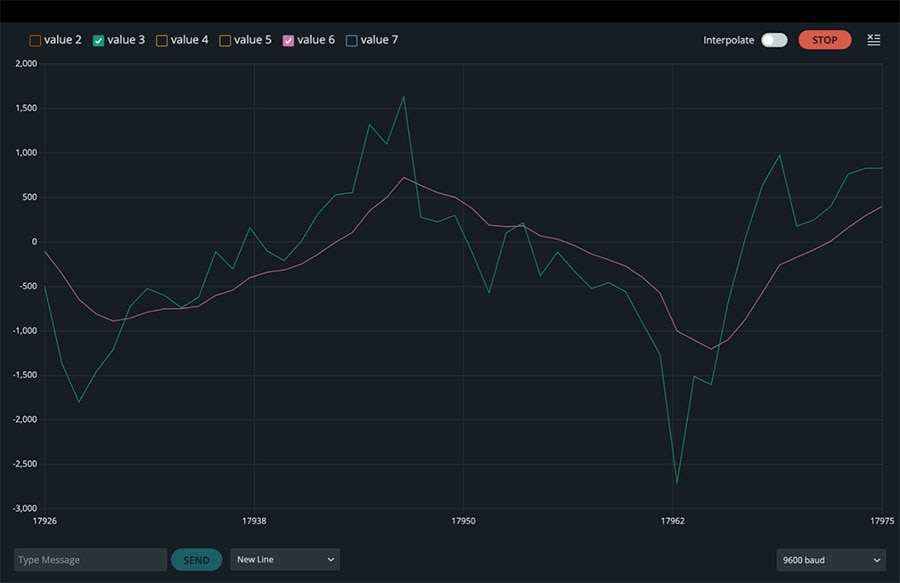Figura 4: Valori di accelerazione grezzi e filtrati nella direzione Y. (Immagine per gentile concessione di Mustahsin Zarif)

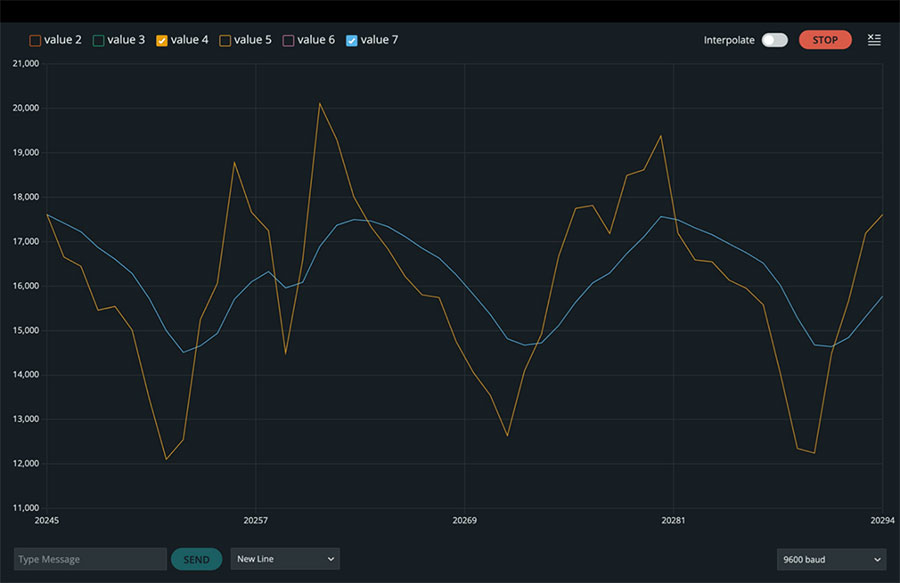Figura 5: Valori di accelerazione grezzi e filtrati nella direzione Z. (Immagine per gentile concessione di Mustahsin Zarif)

Per un codice ancora più intelligente

Ora abbiamo un'idea di come i filtri IIR siano migliori per i controller rispetto ai filtri FIR, perché richiedono un numero molto inferiore di calcoli di addizione e moltiplicazione. Tuttavia, quando implementiamo questo codice, l'addizione e la moltiplicazione non sono gli unici calcoli eseguiti: dobbiamo spostare i campioni ogni volta che arriva un nuovo campione temporale e questo processo, in background, richiede potenza di calcolo. Pertanto, invece di spostare tutti i campioni a ogni intervallo del tempo di campionamento, possiamo avvalerci dell'aiuto di buffer circolari.

Ecco cosa facciamo: abbiamo un puntatore che ricorda l'indice del campione di dati in arrivo. Quindi, ogni volta che il puntatore punta all'ultimo elemento nel buffer, punta al primo elemento del buffer successivo e i nuovi dati sostituiscono i dati che erano stati memorizzati qui in precedenza, poiché questi sono ora i dati più vecchi di cui non abbiamo più bisogno (Figura 6). Di conseguenza, questo metodo consente di tener traccia del campione più vecchio nel buffer e di sostituirlo senza dover spostare i campioni ogni volta per inserire i nuovi dati nell'ultimo elemento dell'array.

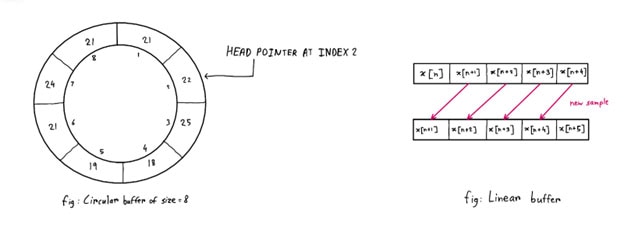Figura 6: Illustrazione esemplificativa di un buffer circolare. (Immagine per gentile concessione di Mustahsin Zarif)

Ecco come appare il codice per un'implementazione del filtro EMA che utilizza buffer circolari. Volete provare a eseguire questa operazione con un giroscopio anziché con un accelerometro? Provate anche a giocare con i coefficienti!

Filtro EMA che utilizza il codice di un buffer circolare:

Copy#include <wire.h>

#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];

float accelYBuffer[BUFFER_SIZE];

float accelZBuffer[BUFFER_SIZE];

int bufferIndex = 0;  

void setup() {

  Serial.begin(115200);

  Wire.begin();
 

  mpu.initialize();


  if (!mpu.testConnection()) {

    Serial.println("MPU6050 connection failed!");

    while (1);

  }

  int16_t ax, ay, az;

  for (int i = 0; i < BUFFER_SIZE; i++) {

    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);

    accelXBuffer[i] = ax / 16384.0;

    accelYBuffer[i] = ay / 16384.0;

    accelZBuffer[i] = az / 16384.0;

  }

}

void loop() {

  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;

  float accelY_float = accelY / 16384.0;

  float accelZ_float = accelZ / 16384.0;

  accelXBuffer[bufferIndex] = accelX_float;

  accelYBuffer[bufferIndex] = accelY_float;

  accelZBuffer[bufferIndex] = accelZ_float;

  bufferIndex = (bufferIndex + 1) % BUFFER_SIZE; //circular buffer implementation 

  float emaAccelX = accelXBuffer[bufferIndex];

  float emaAccelY = accelYBuffer[bufferIndex];

  float emaAccelZ = accelZBuffer[bufferIndex];

  float alpha = 0.2;

  for (int i = 1; i < BUFFER_SIZE; i++) {

    int index = (bufferIndex + i) % BUFFER_SIZE;

    emaAccelX = alpha  accelXBuffer[index] + (1 - alpha)  emaAccelX;

    emaAccelY = alpha  accelYBuffer[index] + (1 - alpha)  emaAccelY;

    emaAccelZ = alpha  accelZBuffer[index] + (1 - alpha)  emaAccelZ;

  }

  Serial.print(accelX_float); Serial.print(",");

  Serial.print(emaAccelX); Serial.print(",");

  Serial.print(accelY_float); Serial.print(",");

  Serial.print(emaAccelY); Serial.print(",");

  Serial.print(accelZ_float); Serial.print(",");

  Serial.println(emaAccelZ);

  delay(100);

}
</mpu6050.h></wire.h>

Conclusione

In questo blog abbiamo discusso la differenza tra filtri IIR e FIR, soffermandoci sulla loro efficienza computazionale. Prendendo un piccolo esempio della riduzione nel numero di operazioni richieste da FIR a IIR, possiamo immaginare quanto saranno efficienti i filtri IIR in applicazioni scalabili, il che è importante per applicazioni in tempo reale con potenza hardware limitata.

Abbiamo anche esaminato un progetto di esempio che utilizza Arduino Uno e una IMU MPU6050, in cui abbiamo implementato un filtro di media mobile esponenziale per ridurre il rumore nei dati sensoriali, continuando comunque a catturare il comportamento del segnale sottostante. Infine, nell'interesse dell'efficienza, abbiamo anche visto un esempio di codice più intelligente che impiega buffer circolari anziché spostare i dati a ogni intervallo temporale.

Nel prossimo blog, utilizzeremo la funzionalità FPGA di Red Pitaya per implementare un circuito digitale a 4 prese intermedie con filtro FIR.