Come usare la potenza di un diagramma di Bode per assicurare stabilità a un circuito

Negli anni '30 del Novecento, Hendrik Wade Bode ideò un approccio intuitivo al guadagno e alla fase, avendo come unico obiettivo la stabilità del circuito. Tale concezione è diventata il diagramma di Bode, una rappresentazione grafica intuitiva del guadagno, della fase e del sistema di retroazione di un circuito o amplificatore nel campo della frequenza.

Vista la sua utilità e importanza, dedicheremo un po' di tempo ad applicare una tecnica di analisi della stabilità di Bode a un amplificatore ad anello aperto e dell'ampiezza (modulo) del fattore di retroazione del circuito in decibel (dB) e della risposta in fase (gradi). In questo blog analizzeremo questi concetti per fornire consigli su come evitare di progettare un circuito rumoroso quando l'obiettivo primario è la stabilità della frequenza.

Per applicare questa tecnica, potrete scaricare una versione stampabile di un diagramma di Bode dalle risorse contenute nel Manuale dell'innovazione DigiKey online.

Diagramma di Bode a un polo

La configurazione del circuito a un polo consente ai segnali V_INc.c. di passare direttamente a V_OUT, mentre a frequenze di ingresso più elevate, V_OUT è uguale a zero decibel (dB). La costruzione del diagramma di Bode è semplice. Le unità dell'asse y rappresentano la frequenza logaritmica e l'asse x rappresenta il guadagno in decibel oppure la fase in gradi. Sono state proposte numerose formule che si possono applicare quando si traccia un diagramma di Bode, ma noi ci limiteremo ad adottare l'approccio più veloce.

La semplicità del diagramma di Bode consiste nel fatto che tutto ciò che serve per tracciare i grafici sono un regolo e la conoscenza di poche regole (Figura 1).

Figura 1: Un diagramma di Bode a un polo che illustra il modulo e la variazione di fase tramite l'utilizzo di linee dritte che descrivono la risposta in frequenza e in fase del circuito. (Immagine per gentile concessione di Bonnie Baker)

I due diagrammi della Figura 1 rappresentano la frequenza rispetto al guadagno e alla fase per una coppia resistore/condensatore a un polo. I campi di frequenza dell'asse x del diagramma superiore e inferiore vanno da 1 Hz a 10 MHz. Il campo dell'asse y del diagramma superiore va da 0 dB a 100 dB, dove il valore del segnale a 1 Hz è uguale a 100 dB. Questo valore è coerente con un fattore di guadagno di 100.000 x V_IN. La curva blu è la risposta di guadagno con un singolo polo a f_P oppure 100°Hz, dove R è uguale a 159 kΩ e C è uguale a 10 nF.

Quando la frequenza aumenta oltre quella del polo (f_P), la curva blu scende a una velocità di -20 dB/decade o -6 dB/ottava. Questa velocità di attenuazione è la prima regola empirica del diagramma di Bode da ricordare: ogni polo del circuito scende a una velocità di -20 dB/decade, iniziando dalla frequenza del polo. Perciò se due poli attenuano V_OUT nello stesso campo di frequenza, la velocità di attenuazione è di -40 dB/decade.

Il diagramma inferiore della Figura 1 rappresenta la fase di questo circuito a un polo. A 1 Hz, la fase della rete R/C è di 0 gradi. A una decade prima di f_P, o in questo caso 10 Hz, la fase a un polo inizia a scendere a -45°/decade verso il suo obiettivo di -90°.

Numerose regole disciplinano la risposta in fase del polo. La seconda regola empirica del diagramma di Bode per il circuito a un polo è che la fase è uguale a -45° a f_P. Le terza e la quarta regola del diagramma di Bode descrivono il punto di attenuazione e di completamento della fase. La fase a un polo inizia a scendere una decade prima della frequenza del polo (f_P) per assestarsi una decade dopo f_P a -90°.

Diagramma di Bode a uno zero

Il diagramma di Bode a uno zero riflette le regole opposte del diagramma di Bode a un polo. Le posizioni si scambiano con gli stessi valori per R e C per evitare tensioni V_INc.c., consentendo alla frequenza più alta di passare per il condensatore (Figura 2).

Figura 2: Un diagramma di Bode a uno zero che illustra il modulo e la variazione di fase. (Immagine per gentile concessione di Bonnie Baker)

Più la frequenza aumenta oltre f_Z, più la curva blu sale di +20 dB/decade. Il diagramma inferiore della Figura 2 rappresenta la fase di questo circuito a uno zero. A una decade prima di f_Z, la fase a uno zero inizia a crescere a una velocità di +45°/decade verso il suo obiettivo di +90°. La fase del circuito zero è uguale a +45° a f_Z.

Per riassumere i valori della Figura 1, la posizione del polo è f_P e il modulo di guadagno dopo f_P ha una pendenza di -20 dB/decade. La fase ha una pendenza di -45°/decade attraverso f_P e inizia la sua attenuazione a 0,1 x f_P, assestandosi a -90° a 10 x f_P. Per riassumere i valori della Figura 2, la posizione zero è f_Z e il modulo di guadagno dopo f_Z ha una pendenza di +20 dB/decade. La fase ha una pendenza di +45°/decade attraverso f_Z e inizia la sua attenuazione a 0,1 x f_Z, assestandosi a +90° a 10 x f_Z.

Diagramma di Bode ad anello aperto di un amplificatore

Il funzionamento in frequenza dell'amplificatore operazionale standard può avere più poli e più zeri nella funzione di trasferimento dai sub-hertz alla frequenza di taglio zero-dB. Non ci sono trucchi di magia nel diagramma di Bode dell'amplificatore, basta seguire le regole (Figura 3).

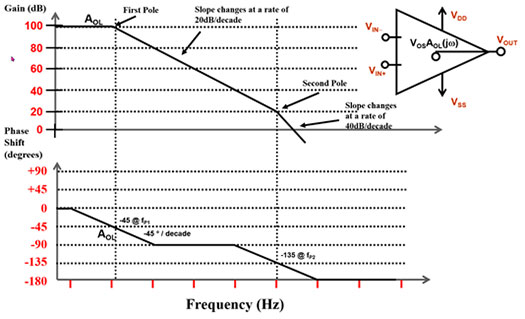Figura 3: Possibile diagramma di Bode di un amplificatore operazionale che illustra il modulo e la variazione di fase. (Immagine per gentile concessione di Bonnie Baker)

La Figura 3 mostra un amplificatore operazionale con due poli (f₁ e f₂) nella funzione di trasferimento. Con i due poli, il guadagno scende a -20 dB/decade ogni volta mentre la fase scende a un totale di -180°.

Ora abbiamo un buon punto di partenza per costruire i diagrammi di Bode, ma se passiamo al mondo reale, dobbiamo fare i conti anche con la presenza di un sistema di retroazione.

Stabilità dei sistemi di amplificazione ad anello chiuso

Se esaminate i circuiti di un amplificatore operazionale, vi accorgerete che presentano sempre una rete di retroazione. La classica rete di retroazione di un amplificatore operazionale ha un elemento di guadagno diretto (A_OL(jω)) e l'elemento di retroazione (β(jω)).

Figura 4: Una classica rete di retroazione di un amplificatore operazionale con un elemento di feed-forward (AOL(jω)) e un elemento di retroazione (β(jω)). (Immagine per gentile concessione di Bonnie Baker)

Nella Figura 4, il guadagno ad anello aperto dell'amplificatore operazionale (A_OL) è relativamente grande e il fattore di retroazione è relativamente piccolo. Questa configurazione restituisce l'uscita al terminale invertente, creando una condizione di retroazione negativa, in cui la retroazione porta sotto controllo l'uscita. Utilizzeremo l'inverso di β o 1/β per determinare la stabilità del circuito di un amplificatore operazionale.

Il modo più semplice per calcolare 1/β consiste nel collocare una sorgente, chiamata V_STABILITY, sull'ingresso non invertente dell'amplificatore operazionale. Questa strategia di calcolo è un ottimo metodo per determinare la stabilità del circuito (Figura 5).

Figura 5: Un circuito non invertente di un amplificatore operazionale a.) e un circuito invertente di un amplificatore operazionale b.) hanno entrambi una sorgente di tensione fittizia V_STABILITY sull'ingresso non invertente per calcolare accuratamente il fattore 1/β del circuito, ossia il guadagno di rumore. (Immagine per gentile concessione di Bonnie Baker)

Esaminando i circuiti della Figura 5, noterete che quelli di retroazione dal terminale non invertente all'uscita sono identici. La posizione della sorgente di tensione V_STABILITY consente di calcolare accuratamente il fattore 1/β del circuito, ossia il guadagno di rumore.

L'analisi della stabilità 1/β utilizza V_STABILITY. Se si presuppone che il guadagno ad anello aperto dell'amplificatore operazionale sia infinito, la funzione di trasferimento di entrambi i circuiti è uguale a:

Equazione 1

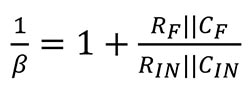Equazione 2

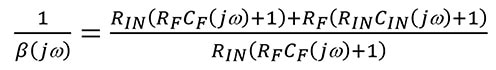Equazione 3

Quando la componente di frequenza dell'equazione 3, jω, è uguale a zero:

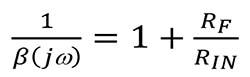Equazione 4

Via via che jω si avvicina all'infinito nell'equazione 3:

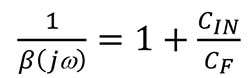Equazione 5

Le frequenze per lo zero di 1/β (f_Z) e il polo (f_P) sono:

Equazione 6

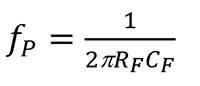Equazione 7

I diagrammi di Bode delle curve di analisi della stabilità 1/β che rispettano l'insieme di regole stabilite sopra sono mostrati nella Figura 6.

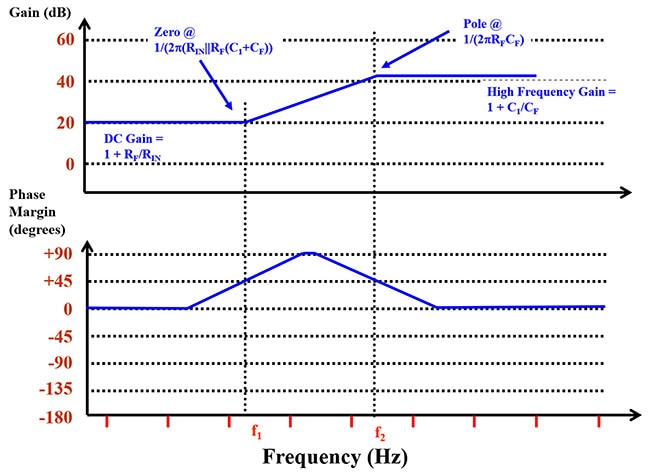Figura 6: La risposta in frequenza di 1/β nella Figura 5 a.) e 5 b.) è identica. Lo zero si genera a una frequenza inferiore e il polo a una frequenza superiore. (Immagine per gentile concessione di Bonnie Baker)

La Figura 6 descrive la risposta in frequenza e di fase di 1/β del circuito dell'amplificatore operazionale, cioè il guadagno di rumore. Questa figura riassume le equazioni da 4 a 7 in forma grafica. Le equazioni 4 e 5 definiscono il guadagno c.c. e ¥ in modo inclusivo. Le equazioni 6 e 7 identificano lo zero e il polo del circuito in modo inclusivo. Le informazioni delle Figure 3 e 6 rappresentano il primo passo per determinare la stabilità del circuito di un amplificatore operazionale definendo la funzione di trasferimento del sistema e la posizione dei poli e degli zeri. Il passo finale consiste nel sovrapporre le Figure 3 e 6 in un unico grafico.

Determinazione della stabilità del sistema

L'intersezione o velocità di chiusura del guadagno ad anello aperto e ad anello chiuso definiscono la variazione di fase del circuito. A linee generali, una velocità di chiusura inferiore o pari a 30 dB indica un circuito stabile. Una velocità di chiusura superiore a 30 dB può portare a una condizione di instabilità del circuito (Figura 7).

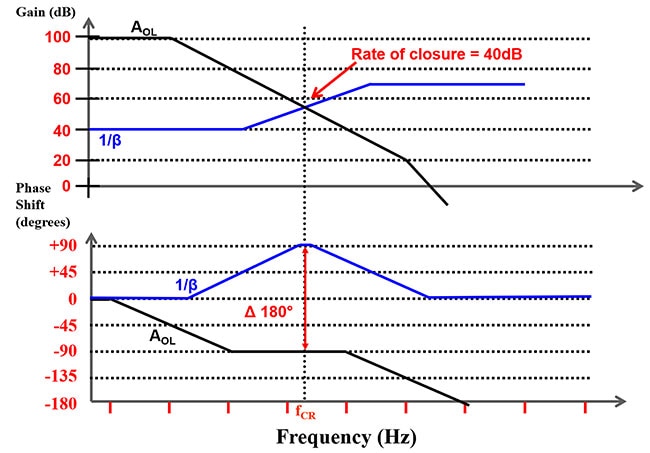Figura 7: Guadagno AOL e risposta in fase dell'amplificatore operazionale sovrapposti con il guadagno 1/β e la risposta in fase. (Immagine per gentile concessione di Bonnie Baker)

Nella Figura 7, la velocità di chiusura tra le curve del guadagno A_OL e 1/β è uguale a 40 dB. Una velocità di chiusura di 40 dB indica una variazione di fase maggiore di 135°, che rivela un circuito instabile. Con questa configurazione, la velocità di chiusura di 180° produce un circuito oscillante.

Esistono molte soluzioni al problema. Si possono variare i valori resistivi o capacitivi spostando le frequenze del polo e dello zero. Alternativamente, si può scegliere un amplificatore operazionale diverso (Figura 8).

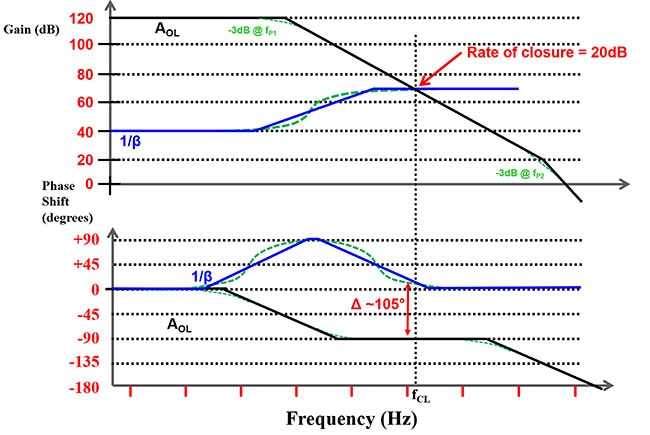Figura 8: Utilizzo di un amplificatore operazionale con una larghezza di banda più alta di quella dell'amplificatore operazionale della Figura 7 senza cambiare le frequenze dello zero e del polo. (Immagine per gentile concessione di Bonnie Baker)

Nella Figura 8, la larghezza di banda dell'amplificatore operazionale è di circa due decadi più alta senza alcuna conseguenza per la rete 1/β. Le linee verdi tratteggiate riflettono i calcoli reali e forniscono un diagramma di Bode più realistico. L'aumento della larghezza di banda dell'amplificatore cambia la velocità di chiusura da 40 dB a 20 dB. La variazione di fase risultante è ora ~105°, che indica un circuito stabile.

Le linee verdi a puntini della Figura 8 vanno oltre il disegno a matita di un diagramma di Bode e includono la risposta nel mondo reale.

Misurazione del guadagno e della fase del circuito

Per misurare il guadagno e la fase del circuito di un amplificatore sono necessari un generatore di funzioni, che fornisce il segnale di ingresso, e a un analizzatore di rete (Figura 9). È illustrato il generatore di funzioni RF spazzolato a 3 GHz analogico LS3081B di Tabor Electronics.

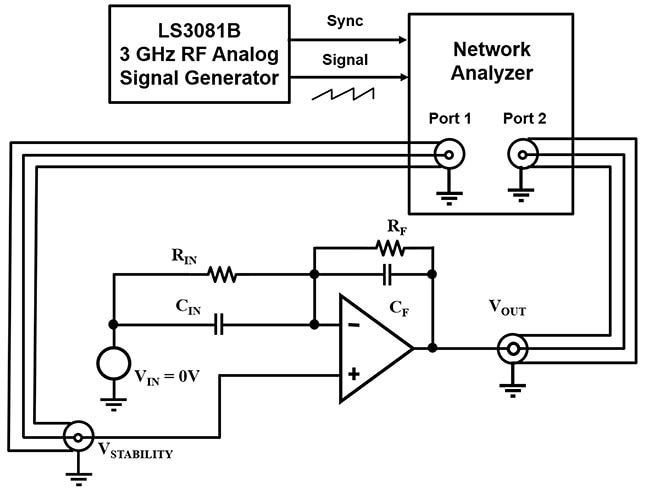Figura 9: Configurazione della misurazione di guadagno e fase per il circuito dell'amplificatore invertente della Figura 5 b.). (Immagine per gentile concessione di Bonnie Baker)

Nella Figura 9, l'applicazione del segnale di ingresso del generatore di funzioni avviene sulla porta 1 del nodo V_STABILITY. Il segnale si propaga attraverso il circuito dell'amplificatore fino all'uscita del circuito (V_OUT), dove l'analizzatore di rete registra il segnale alla porta 2 e lo confronta con quello alla porta 1 del generatore di funzioni.

Conclusione

Quando si tratta di progettare circuiti stabili per gli amplificatori operazionali, il diagramma di Bode è uno strumento estremamente utile da aggiungere alla vostra cassetta degli attrezzi. La potenza del diagramma di Bode si palesa quando cominciate ad analizzare i circuiti a più poli e più zeri, dove la velocità di chiusura tra il guadagno ad anello aperto dell'amplificatore e la rete di retroazione definisce velocemente la stabilità del circuito.

Questo blog potrà aiutarvi a padroneggiare i diagrammi di Bode mostrandovi l'uso di un regolo su carta millimetrata per stimare il guadagno rispetto alla fase di un circuito a un polo e uno zero di primo ordine, sebbene il modo migliore per imparare rimanga sempre la pratica. Vi suggeriamo nuovamente di scaricare una versione stampabile di un diagramma di Bode dalle risorse contenute nel Manuale dell'innovazione DigiKey online.