Perché e come usare i filtri digitali per conversioni analogico/digitale ad alta risoluzione e ad alta velocità

Il nostro è ancora analogico, ma l'elettronica digitale è sempre più onnipresente - e per una buona ragione. Mentre il digitale risolve molti problemi con approcci algoritmici, anche i migliori algoritmi digitali hanno delle carenze nel trattare con entità del mondo reale che esistono nel dominio analogico. Ciò vale soprattutto nelle applicazioni che richiedono l'acquisizione di dati ad alta velocità e ad alta risoluzione, come la strumentazione, il controllo dei motori e i sistemi di acquisizione dati.

Il problema per i progettisti che cercano di acquisire ed elaborare tali segnali del mondo reale è la necessità di entrare nel dominio digitale il più presto possibile senza compromettere le informazioni del segnale. La soluzione viene da un semplice algoritmo di calcolo della media (per ridurre il rumore) con un filtro passa-basso analogico (LPF) front-end. Con queste tecniche, un dispositivo adatto può fornire una conversione ad alta risoluzione e ad alta velocità con filtraggio analogico e digitale.

Questo articolo discute brevemente i problemi associati all'ottenimento di conversioni ad alta risoluzione e ad alta velocità con un convertitore analogico/digitale (ADC) con registro ad approssimazioni successive (SAR) utilizzando un LPF analogico e un filtro a media digitale e spiega perché questa combinazione di filtri è una buona opzione per la maggior parte delle applicazioni. Introduce poi l'ADC SAR a otto canali AD7606C-18 di Analog Devices e mostra come trarre vantaggio dalla sua velocità di conversione di 1 Msps, dall'array di convertitori a campionamento simultaneo e dalle flessibili funzioni del filtro digitale.

Per mostrare come trarre le migliori prestazioni complessive, questo articolo combina AD7606C-18 con il riferimento di tensione ADR4525 a bassissimo rumore e alta precisione, anch'esso di Analog Devices, per migliorare la precisione SAR necessaria per le conversioni a 18 bit.

Filtri analogici e digitali

Se un ingegnere analogico e un ingegnere digitale si mettono a discutere di filtri, l'ingegnere digitale potrebbe liquidare quello analogico in poche parole. Ma sarebbe un errore. La norma nel filtraggio per la conversione analogico/digitale (A/D) prevede un LPF analogico prima del filtro digitale (Figura 1).

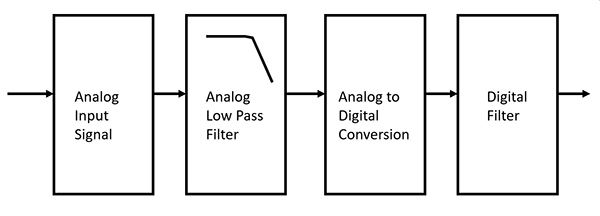Figura 1: Diagramma a blocchi di una catena di segnale analogico/digitale con il filtro analogico prima del filtro digitale. (Immagine per gentile concessione di DigiKey)

Dopo che l'LPF analogico attenua le frequenze superiori alla larghezza di banda di interesse, l'ADC converte il segnale in una parola digitale. Dopodiché, il filtro digitale può operare sul segnale entro la larghezza di banda di interesse.

Filtri analogici in ambienti di acquisizione dati

L'importanza dell'LPF analogico viene alla luce all'uscita dell'ADC. Qualsiasi segnale che passa attraverso l'ADC ha una grandezza e una frequenza associate. All'uscita dell'ADC, la grandezza del segnale rimane affidabile se la frequenza del segnale è inferiore alla larghezza di banda d'ingresso dell'ADC. Anche se la conversione A/D conserva la grandezza del segnale, ciò non vale per le frequenze del segnale. Si può osservare un cambiamento nelle frequenze al di sopra di ½ della frequenza di campionamento dell'ADC, f_S, nota anche come la frequenza di campionamento di Nyquist (Figura 2).

Figura 2: Nel grafico (A), la rappresentazione della trasformata di Fourier veloce (FFT) di un segnale di ingresso ha cinque componenti di frequenza. Dopo una conversione A/D, la rappresentazione FFT nel grafico (B) mostra tutti e cinque i segnali che si verificano sotto la metà della frequenza di campionamento dell'ADC (f_S). (Immagine per gentile concessione di DigiKey)

Nella Figura 2, entrambi i grafici FFT usano una frequenza logaritmica sull'asse x e una tensione o grandezza lineare sull'asse y. Nel grafico (A), la rappresentazione FFT del segnale analogico mostra il segnale di ingresso di un ADC con più segnali o rumore sopra la metà della frequenza di campionamento ADC, o f_S/2.

Confrontando questi due grafici, è utile seguire i cinque segnali FFT. Dopo una conversione ADC, le grandezze del segnale originale rimangono le stesse, ma le frequenze sopra la metà della frequenza di campionamento in (A) sono "invertite" di nuovo sotto f_S/2 in (B). Questo fenomeno è noto come sovrapposizione spettrale (aliasing) del segnale. Per acquisire accuratamente il segnale, la frequenza di campionamento f_S dell'ADC deve essere maggiore di due volte f_MAX, dove f_MAX è uguale alla larghezza di banda utilizzabile del segnale, secondo il teorema di campionamento di Shannon-Nyquist.

Si può vedere come gli ADC impiantano permanentemente rumore e segnali indesiderati nel segnale di uscita digitale. Questo cambiamento rende impossibile distinguere la differenza tra i segnali in banda e quelli fuori banda all'uscita del convertitore.

Ci si potrebbe aspettare che ci sia un percorso avanti e indietro tra queste due rappresentazioni FFT. Una volta che questa trasformazione è avvenuta, però, non c'è modo di tornare indietro e annullarla. Sfortunatamente, la matematica non supporta questo tipo di transizione avanti e indietro.

Tornando al dibattito analogico/digitale: un filtro digitale è senza dubbio in grado di applicare la media calcolata, il filtraggio a risposta impulsiva finita (FIR) o infinita (IIR) e quindi di ridurre il rumore del sistema. Tuttavia, ogni filtro digitale richiede una quantità significativa di sovracampionamento (il processo di campionamento di un segnale a una frequenza di campionamento significativamente superiore alla velocità dei dati di uscita finale) che richiede tempo, potenza e riduce la velocità di campionamento dell'ADC. Il filtro digitale e la funzione del convertitore non superano mai i fenomeni del segnale. È meglio ridurre semplicemente il rumore ad alta frequenza dall'inizio, anche con un rudimentale LPF analogico del primo ordine.

Filtri a media digitale

Gli ADC SAR migliorano la loro misurazione del rumore c.c. con un filtro a media digitale. Questo filtro digitale acquisisce conversioni multiple con una scala temporale coerente per aumentare il numero di bit. Gli utenti ADC usano algoritmi di calcolo della media con il loro controller, processore o un motore su chip che acquisisce diversi campioni del convertitore. Il processo "livella" il gruppo di conversione e migliora la risoluzione effettiva attraverso la riduzione del rumore del sistema.

L'implementazione del livellamento dei dati convertiti comporta acquisizioni multiple del segnale a una frequenza di campionamento costante e il calcolo della media di un numero di campioni predeterminato. Il processo di calcolo della media è ben noto. La somma dei risultati ADC (campioni successivi, x) divisa per il numero di campioni (N) produce un valore medio (Equazione 1).

 Equazione 1

Questo processo riduce la velocità dei dati in uscita di un fattore N ma aumenta il tempo di assestamento del sistema.

La deviazione standard dei campioni rumorosi mediati (σ_avg) è la deviazione standard del segnale originale (σ_sig) divisa per la radice quadrata di N (Equazione 2).

 Equazione 2

I campioni successivi, compreso il rumore non correlato, porteranno a una maggiore riduzione del rumore in una media del segnale costante. Ogni campione consecutivo mediato fa sì che il rapporto segnale/rumore (SNR) migliori se il segnale è c.c. e la componente di rumore è casuale.

Il miglioramento del SNR è proporzionale alla radice quadrata del numero di campioni mediati. Una media di quattro campioni di segnale c.c. (⁴¹) aumenterà la risoluzione effettiva del convertitore di uno con un aumento di 6 dB nell'SNR. Una media di 16 o 4² campioni aumenta la risoluzione effettiva di due e l'SNR di 12 dB. Con questa logica, una dimensione di gruppo di 4^N aumenterà il numero di bit effettivi di una conversione di N, portando il rumore del sistema a zero e il valore di SNR a infinito.

La varianza Allan

Un valore SNR infinito è assurdo, ovviamente. Nel mondo reale, l'acquisizione del numero necessario di campioni richiede tempo, durante il quale il sistema può cambiare in termini di gradi di deriva.

La varianza Allan, conosciuta come varianza a due campioni, misura la stabilità della frequenza in clock, oscillatori, ADC e amplificatori, mostrando il cambiamento nel rumore all'aumentare del numero di campioni usati nel calcolo della media di un segnale. Lo strumento di analisi statistica della varianza Allan determina il numero massimo di campioni necessari considerato ottimale per un particolare sistema, stimando così la stabilità evidenziando la deriva della frequenza o gli effetti della temperatura.

Ad esempio, i dati in un sistema da un ADC nel tempo possono mostrare spostamenti come mostra la Figura 3.

Figura 3: I 30.000 punti di dati di uscita ADC acquisiti in nove minuti mostrano una leggera deriva nei dati in quel periodo, causando un deterioramento nel calcolo della varianza Allan. (Immagine per gentile concessione di Electronic Design)

L'algoritmo della varianza prende più lotti di medie sempre più lunghe e valuta il rumore risultante di ogni lotto (Figura 4).

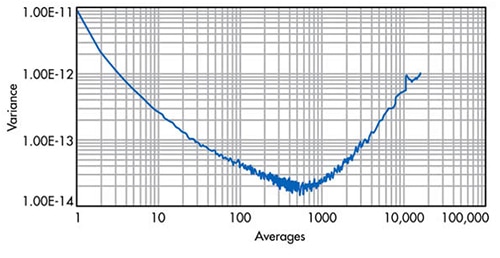Figura 4: Calcolo della varianza di Allan applicato ai punti di dati della Figura 3. Alla media di 500 punti, questo particolare sistema ADC acquisisce 4,48 bit o un aumento dell'SNR di 27 dB. (Immagine per gentile concessione di Electronic Design)

La Figura 4 dimostra che la varianza minima dei punti di dati di questo particolare sistema si verifica a circa 500 medie di uscita ADC - il numero ottimale di medie di campioni per la riduzione del rumore. Alla media di 500 punti, questo sistema ADC acquisisce 4,48 bit o un aumento dell'SNR di 27 dB. Prima e oltre il 500° punto medio, i risultati peggiorano nella Figura 4 perché la deriva dei dati diventa un fattore maggiore. Le variabili che hanno un impatto sui calcoli della varianza Allan possono essere il tempo, la stabilità del segnale, la deriva, le variazioni dell'alimentazione e l'invecchiamento del prodotto. Se è in uso un filtro a media digitale, è prudente valutare il sistema complessivo con lo strumento della varianza Allan.

Soluzione del mondo reale

I convertitori SAR possono offrire funzioni di amplificatore a guadagno programmabile (PGA) e filtro digitale per migliorare la risoluzione effettiva e la tensione del bit meno significativo (LSB). Ad esempio, AD7606C-18 di Analog Devices è un sistema di acquisizione dati (DAS) A/D a 18 bit, 1 Msps di campionamento simultaneo, con otto canali, ognuno dei quali contiene una protezione del morsetto di ingresso analogico, un PGA, un LPF e un ADC SAR a 18 bit.

Il dispositivo ha anche buffer di ingresso analogico con un'impedenza di ingresso di 1 MΩ e configurazioni programmabili di tensione di ingresso bipolare differenziale, bipolare e unipolare a terminazione singola. AD7606C-18 permette il collegamento di otto sensori di ingresso indipendenti o canali di segnale.

Il filtro digitale AD7606C-18 ha una modalità di sovracampionamento che calcola la media di campioni ripetitivi da 1 a 256 (4⁴). Secondo lo strumento della varianza Allan, questa caratteristica di sovracampionamento migliora le prestazioni di rumore all'uscita digitale del convertitore. Il riferimento di tensione di precisione a basso rumore, di 2,5 V ADR4525 completa il sistema DAS AD7606C-18 con un coefficiente di temperatura massima di 1 ppm/°C e 1 mV di rumore di uscita tipico da picco a picco (Figura 5).

Figura 5: 'ADC SAR ADR4525 con riferimento di tensione di precisione di 2,5 V. Gli induttori con LPF del primo ordine sui canali di ingresso da V1 a V8 campionano simultaneamente tutti gli otto canali. (Immagine per gentile concessione di Analog Devices)

Come mostra la Figura 5, questo tipo di array SAR ad alta impedenza di ingresso può interfacciarsi direttamente con i sensori senza i tipici amplificatori di pilotaggio esterni. Lo stadio di guadagno del sensore esterno potrebbe anche essere superfluo. Contemporaneamente, il convertitore SAR ha uno stadio interno PGA e LPF che fornisce l'elaborazione del segnale, seguito da un filtro a media digitale per ridurre ulteriormente il rumore fornendo risoluzioni effettive più elevate. Un tale DAS può offrire una risoluzione effettiva di 17,1 bit con una velocità di conversione di 3,9 ksps. All'altra estremità dello spettro della velocità di conversione, questo dispositivo offre una risoluzione effettiva di 15 bit con una velocità di conversione di 1 Msps.

La velocità di conversione maggiore di AD7606C-18 è di 1 Msps con un sovracampionamento pari a uno. Se il sovracampionamento dei canali del convertitore è due, o fa la media dei campioni di un canale due volte, la velocità di conversione è la metà della velocità massima di conversione a 500 ksps. Per un sovracampionamento uguale a quattro, o 4¹ come numero di campioni mediati, la velocità di conversione di quel canale è di 250 ksps, e così via. Per ognuno degli otto canali, il sistema con un valore di sovracampionamento di 256 fornisce un intervallo sbilanciato di ±10 V, 17,1 bit di risoluzione effettiva (SNR=105 dB), con una velocità di conversione di 3,9 ksps (Tabella 1).

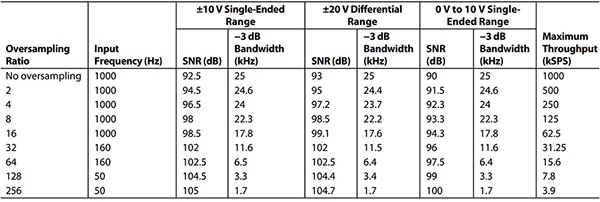Tabella 1: Prestazioni di sovracampionamento, modalità di larghezza di banda bassa di AD7606C-18. (Tabella per gentile concessione di Analog Devices)

La formula di conversione da SNR a risoluzione effettiva (numero effettivo di bit, o ENOB) è mostrata nell'Equazione 3.

 Equazione 3

All'altra estremità dello spettro della velocità di conversione, con un fattore di sovracampionamento di 1, questo dispositivo fornisce una risoluzione effettiva di 15 bit (SNR=92,5 dB) con una velocità di conversione di 1 Msps (Tabella 1).

AD7606C-18 offre ulteriori miglioramenti. Poiché ha otto ADC SAR separati su chip, tutti gli otto canali hanno una funzione di campionamento simultaneo. Con questa funzione, è possibile implementare il filtro digitale per ottenere contemporaneamente un'alta risoluzione o un'alta velocità su tutti i canali. Inoltre, tutti i canali hanno capacità di calibrazione e diagnostica.

Ad esempio, la calibrazione di fase del sistema AD7606C-18 rileva la discrepanza del filtro di ingresso discreto. Questa preziosa caratteristica identifica qualsiasi discrepanza sui componenti discreti o nel sensore utilizzato che può causare errori di fase tra i canali campionati simultaneamente. La modalità software del dispositivo compensa la discrepanza di fase canale per canale, ritardando l'istante di campionamento di un singolo canale.

La calibrazione del guadagno del sistema rileva le discrepanze delle resistenze del filtro di ingresso discreto. Questa capacità aiuta a superare le discrepanze del resistore esterno. La modalità software compensa l'errore di guadagno canale per canale scrivendo il valore del resistore in serie utilizzato sul registro corrispondente.

La calibrazione dell'offset di sistema accetta gli offset del segnale di ingresso durante l'attività di calibrazione. Il software può regolare l'offset del sensore esterno di ogni canale o qualsiasi offset di discrepanza della coppia del resistore esterno.

Per un'applicazione specifica, la scheda EVAL-AD7606SDZ per AD7606 è dotata di un software per assistere nelle valutazioni con la programmazione del dispositivo, così come forma d'onda, istogramma e acquisizione FFT (Figura 6).

Figura 6: La scheda di valutazione AD7606 (sinistra) collegata alla scheda SDP (destra), che permette di controllare la scheda di valutazione attraverso la porta USB di un PC. (Immagine per gentile concessione di Analog Devices)

Il software della scheda di valutazione permette all'utente di configurare il valore di sovracampionamento di ogni canale, l'intervallo di ingresso, il numero di campioni e la selezione del canale attivo. Inoltre, questo software permette anche di salvare e aprire file con i dati dei test.

Conclusione

Nonostante il passaggio al digitale, il nostro è ancora un mondo analogico e i progettisti hanno bisogno di un'elettronica analogica per risolvere problemi di conversione ad alta risoluzione e ad alta velocità. Come mostrato, la semplice combinazione di un LPF analogico e di un filtro a media digitale, implementato con il numero appropriato di campioni mediati, migliora notevolmente le prestazioni di un convertitore SAR a 1 Msps.