I principi base dei filtri passa-basso antialiasing (e perché devono essere abbinati all'ADC)

Se non sono protetti, i sistemi base di acquisizione dei dati campionati - per IoT, case intelligenti o controlli industriali - saranno interessati da imprecisioni dovute all'aliasing, in cui la sottocampionamento dell'ingresso analogico genera segnali spuri. L'aliasing fa flettere le componenti di segnale a frequenze superiori a quella di Nyquist (metà della frequenza di campionamento) nello spettro della banda base, per cui non possono essere separate dai segnali desiderati e danno luogo a errori. Inoltre, il rumore al di sopra della frequenza di Nyquist viene miscelato anche in basso nella banda base, abbassando il rapporto segnale/rumore (SNR) dei segnali in banda base desiderati.

La soluzione per impedire l'aliasing consiste nel limitare la banda dei segnali di ingresso, limitando tutte le componenti di segnale di ingresso al di sotto della metà della frequenza di campionamento del convertitore analogico/digitale (ADC). A tale fine si utilizzano filtri passa-basso analogici chiamati filtri antialiasing, che devono limitare la banda senza aggiungere distorsione del segnale, rumore o variazioni di ampiezza con la frequenza. I progetti di filtri passa-basso antialiasing devono fornire un roll-off rapido con un'attenuazione della banda di arresto sufficiente per ridurre nettamente le ampiezze del segnale al di sopra della frequenza di Nyquist.

Questo articolo prende in esame i criteri di progettazione di filtri passa-basso antialiasing e perché e come abbinarli accuratamente alle specifiche dell'ADC. Mostrerà quindi come possono essere implementati con filtri a condensatore commutato o attivo utilizzando dispositivi di esempio di Analog Devices.

Che cos'è l'aliasing?

L'aliasing si verifica quando un sistema acquisisce i dati a una frequenza di campionamento insufficiente. Se un segnale contiene frequenze superiori a quella di Nyquist, queste vengono mischiate con la frequenza di campionamento nel campionatore del convertitore e mappate su frequenze inferiori a quella di Nyquist. Durante il campionamento vengono così mischiati segnali diversi, che risultano indistinguibili l'uno dall'altro (ovvero, alias l'uno dell'altro) (Figura 1).

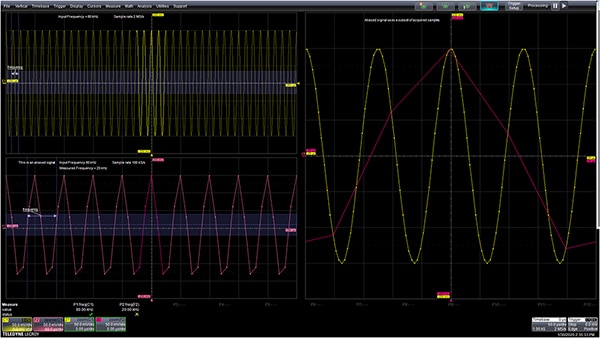Figura 1: Un esempio di aliasing. Un'onda sinusoidale a 80 kHz campionata a 2 Msps (in alto a sinistra) non presenta nessun aliasing. Se la frequenza di campionamento viene ridotta a 100 ksps (in basso a sinistra), il segnale viene interpretato come avente una frequenza di 20 kHz. Sia i segnali campionati correttamente che quelli alias appaiono sovrapposti nella vista ingrandita (a destra). I puntini su quella traccia mostrano le posizioni dei campioni. Tenere presente che il segnale alias utilizza un sottoinsieme dei dati campionati correttamente. (Immagine per gentile concessione di Digi-Key Electronics)

Il segnale mostrato nella griglia in alto a sinistra è un'onda sinusoidale a 80 kHz campionata a 2 Msps. A 2 Msps la frequenza di Nyquist è di 1 MHz; il segnale è ben al di sotto di questo valore. La griglia in basso a sinistra mostra cosa accade quando la frequenza di campionamento viene ridotta a 100 ksps. La frequenza di Nyquist è ora di 50 kHz, quella del seno di 80 kHz è superiore a essa e subisce l'aliasing.

Sul lato destro dell'immagine, i segnali correttamente campionati e quelli alias vengono espansi e sovrapposti in orizzontale e i campioni reali sono indicati da un punto. Tenere presente che il segnale alias contiene un sottoinsieme dei campioni del segnale campionato a 2 Msps. Il campionamento consiste in un'operazione di miscelazione il cui risultato è costituito dalla somma e dalla differenza dei segnali di ingresso e della frequenza di campionamento.

Con una frequenza di campionamento di 100 ksps e una frequenza di segnale di 80 kHz, la frequenza della differenza è di 20 kHz. Le misure di frequenza di entrambi i casi sono riportate sotto le griglie di visualizzazione. Il parametro P1 legge la frequenza del segnale correttamente campionato di 80 kHz, mentre la frequenza del segnale influenzato dall'aliasing è di 20 kHz.

Progettazione di un filtro passa-basso antialiasing

Quando si progetta un filtro antialiasing, il primo passo è determinare la larghezza di banda necessaria nel sistema di acquisizione. Questo valore determina la frequenza di taglio del filtro passa-basso. Le frequenze di taglio del filtro sono tipicamente impostate a -3 decibel (dB), o mezzo punto di potenza. Questa è la frequenza in cui l'ampiezza del segnale filtrato scende a 0,707 dell'ampiezza in c.c. Se il progetto del sistema di acquisizione richiede una risposta in frequenza più piatta, il taglio potrebbe essere definito con un valore di attenuazione più basso, ad esempio -1 dB. Un'ampiezza della frequenza di taglio maggiore dà più importanza al roll-off della risposta in frequenza del filtro antialiasing.

Dopo aver determinato la larghezza di banda del sistema di acquisizione, si può impostare la frequenza di campionamento. La frequenza di campionamento minima teorica è il doppio della larghezza di banda del sistema di acquisizione. Tuttavia, nella realtà questo limite teorico non è una buona frequenza di campionamento, poiché un filtro antialiasing reale non può attenuare i segnali al di sopra della frequenza di taglio con la stessa rapidità di un perfetto filtro teorico. Ciò significa che la frequenza di campionamento dovrebbe essere più alta. In questo caso però, i requisiti di memoria aumentano con l'aumentare della frequenza di campionamento. Quando la memoria era costosa, la frequenza di campionamento veniva tenuta il più vicino possibile alla zona di Nyquist - di solito tra 2,5 e quattro volte la larghezza di banda in ingresso. La riduzione dei costi della memoria facilita questo requisito, per cui si può avere una frequenza di campionamento più alta. Non è insolito arrivare a cinque o dieci volte la larghezza di banda.

Prendiamo in esame un progetto per un sensore a ultrasuoni che richiede una larghezza di banda di acquisizione di 100 kHz. La frequenza di campionamento potrebbe andare da 500 kHz a 1 MHz.

Ora si può scegliere l'ADC. Per il nostro esempio, si può scegliere un convertitore ad approssimazioni successive a 12 bit con una frequenza di campionamento di 1 Msps, come LTC2365ITS8#TRMPB di Analog Devices. La sua risoluzione a 12 bit fornisce una gamma dinamica teorica di 72 dB. Questo ADC ha prestazioni dinamiche eccellenti che includono una specifica SINAD (segnale-rumore e distorsione) di -72 dB e un SNR di -73 dB, entrambi a una frequenza di campionamento di 1 Msps (Figura 2).

Figura 2: Diagramma a blocchi e prestazioni SINAD dell'ADC ad approssimazioni successive a 12 bit LTC2365ITS8#TRMPB di Analog Devices. (Immagine per gentile concessione di Analog Devices)

Funzionando a una frequenza di campionamento di 1 Msps, la frequenza di Nyquist è di 500 kHz. L'uscita del filtro passa-basso a 100 kHz deve avere un'attenuazione della banda di arresto per portare le componenti del segnale al di sopra della zona di Nyquist fino al rumore di fondo dell'ADC, in questo caso maggiore di -73 dB per frequenze superiori a 500 kHz.

Scelta del tipo di filtro

Esistono molti tipi o configurazioni di filtri passa-basso. I più usati sono i filtri Butterworth, Chebyshev e Bessel. Hanno risposte in frequenza diverse e offrono alcune importanti distinzioni a seconda dell'applicazione (Figura 3).

Figura 3: Confronto delle risposte in frequenza dei filtri Butterworth (grigio), Chebyshev (blu) e Bessel (arancione). I tipi di filtro si differenziano per planarità del passa-banda, ritardo di fase e pendenza della regione di transizione. (Immagine per gentile concessione di Digi-Key Electronics)

Le risposte dei tre filtri mostrate hanno caratteristiche specifiche. Ad esempio, il filtro Butterworth ha una risposta in ampiezza estremamente piatta. Ciò significa che offre la risposta di guadagno più piatta con frequenza nel passa-banda con un moderato roll-off nella regione di transizione.

I filtri Bessel offrono un ritardo uniforme per un ritardo di gruppo costante. Ciò significa che hanno una risposta in fase lineare con frequenza e risposta ai transitori eccellente per un ingresso a impulsi. Questa ottima risposta in fase va però a scapito della planarità del passa-banda e comporta un'attenuazione più lenta del roll-off iniziale oltre il passa-banda.

I filtri Chebyshev sono progettati per avere un roll-off più ripido nella regione di transizione, ma hanno più ripple nel passa-banda. I progetti che utilizzano questo tipo di filtro si basano in genere su un ripple massimo specifico. Ad esempio, se il limite di ampiezza della frequenza di taglio è di -1 dB, la specifica del ripple di solito sarebbe impostata al massimo su 1 dB.

La risposta di questi filtri a un impulso nel dominio temporale è utile per capire la scelta del tipo di filtro appropriato (Figura 4).

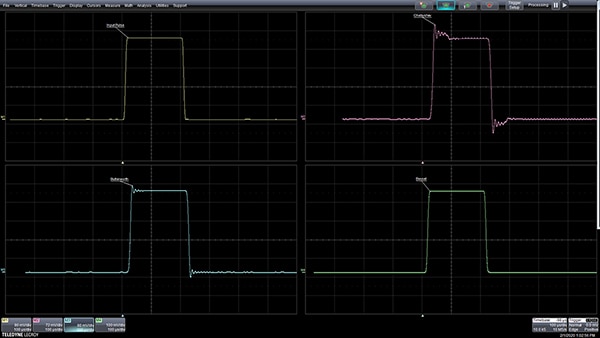Figura 4: La risposta del filtro a un impulso di ingresso (in alto a sinistra) mostra le differenze nella risposta all'impulso nel dominio temporale dei tipi di filtri Chebyshev (in alto a destra), Butterworth (in basso a sinistra) e Bessel (in basso a destra). (Immagine per gentile concessione di Digi-Key Electronics)

La risposta in fase lineare del filtro Bessel con frequenza passa l'impulso con una distorsione minima, ma non ha la planarità di ampiezza del filtro Butterworth o il taglio netto dei filtri Chebyshev. Il tipo di filtro selezionato dipende dall'applicazione:

• Se la preoccupazione principale è l'accuratezza dell'ampiezza, è opportuno scegliere il filtro Butterworth
• Se la frequenza di campionamento desiderata è vicina alla larghezza di banda del segnale, sarebbe indicato il filtro Chebyshev
• Se si è principalmente interessati alla fedeltà dell'impulso, la scelta migliore è il filtro Bessel

Ordine del filtro

L'ordine del filtro si riferisce alla complessità del progetto del filtro. Il termine si riferisce al numero di elementi reattivi, come i condensatori, presenti nel progetto. Rappresenta anche il numero di poli nella funzione di trasferimento del filtro.

L'ordine di un filtro influenza la ripidezza del roll-off della regione di transizione e quindi la larghezza di questa regione. Un filtro del primo ordine ha un roll-off di 6 dB per ottava, o 20 dB per decade. Un filtro dell'ennesimo ordine avrà un tasso di roll-off di 6×n dB/ottava o 20×n dB/decade. Quindi, un filtro dell'8° ordine ha un tasso di roll-off di 48 dB per ottava o 160 dB per decade.

Utilizzando come esempio il progetto del sensore a ultrasuoni descritto in precedenza, tutti i segnali superiori a 100 kHz devono essere attenuati di almeno -73 dB dalla frequenza di Nyquist di 500 kHz. Il filtro dell'8° ordine attenua i segnali di circa -98 dB a 500 kHz (Figura 5). Un filtro del 6° ordine attenua un segnale fuori banda a 500 kHz di circa -83 dB. Quindi, ai fini del nostro esempio, un filtro del 6° ordine sarebbe adeguato, ma uno dell'8° ordine fornirebbe un'ampiezza ancora più bassa per i segnali fuori banda. Se i costi sono gli stessi, si dovrebbe scegliere il filtro dell'8° ordine. Parleremo ancora di questi pro e contro più avanti, quando si discuterà dei componenti.

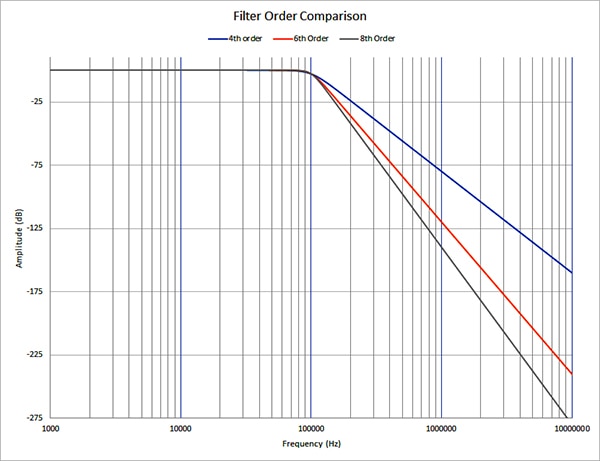Figura 5: Confronto del roll-off delle risposte del filtro del 4° ordine (blu), del 6° (arancione) e dell'8° (grigio). (Immagine per gentile concessione di Digi-Key Electronics)

L'ordine di un filtro può essere incrementato mediante il collegamento in cascata di più sezioni. Ad esempio, si possono mettere in cascata due filtri passa-basso del 2° ordine per ottenere un filtro passa-basso del 4° ordine, e così via. Il rovescio della medaglia, quando si mettono in cascata più filtri attivi, è un aumento del consumo energetico, del costo e delle dimensioni.

La scelta di un filtro del 6° o 8° ordine dipenderà anche dalla configurabilità del filtro selezionato. I circuiti integrati dei filtri configurati come filtri quadrupli di 2° ordine possono implementare un filtro del 6° ordine, ma i circuiti integrati del filtro configurati come doppi filtri di 4° ordine dovrebbero implementare un filtro dell'8° ordine.

Componenti dei filtri

I filtri antialiasing per le frequenze acustiche e ultrasoniche possono essere implementati utilizzando filtri a condensatore attivi o commutati. In genere, i risultati dei due tipi di filtro sono molto simili. Nelle applicazioni che utilizzano ADC ad altissima risoluzione di 16 bit o più, si potrebbe preferire il filtro attivo per il minore potenziale di rumore. I filtri a condensatore commutati, che richiedono un segnale di clock, hanno un maggiore potenziale di rumore dovuto alla diafonia dal segnale di clock.

La famiglia LTC1563 di Analog Devices offre filtri attivi a 4 poli o del 4° ordine che utilizzano un singolo resistore per controllare la frequenza di taglio. La famiglia offre configurazioni con filtro Butterworth o Bessel. LTC1563-2 è un filtro configurato Butterworth a 4 poli con una frequenza di taglio massima di 256 kHz. Il circuito integrato di questo filtro può essere collegato in cascata per ottenere una risposta passa-basso dell'8° ordine (Figura 6).

Figura 6: Un filtro Butterworth dell'8° ordine, a 20 kHz, implementato utilizzando due dispositivi LTC1563-2 di Analog Devices. (Immagine per gentile concessione di Analog Devices)

Se l'applicazione richiede una frequenza di taglio variabile, LTC1564IG#TRPBF di Analog Devices è una scelta valida. Questo filtro passa-basso dell'8° ordine ha una larghezza di banda controllata digitalmente con un bus di controllo a 4 bit per variare la frequenza di taglio da 10 kHz a 150 kHz in passi di 10 kHz. Anche il guadagno è programmabile digitalmente. Il filtro ha una gamma dinamica di 122 dB ed è destinato a sistemi di acquisizione con risoluzione da 16 a 20 bit (Figura 7).

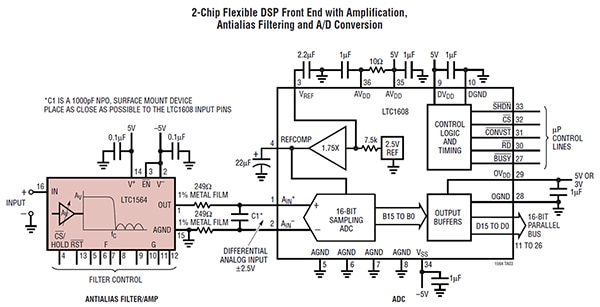Figura 7: Sistema di acquisizione a 16 bit, 500 ksps utilizzando solo due CI. LTC1564IG#TRPBF fornisce una larghezza di banda variabile fino a 150 kHz e un guadagno fino a 24 dB. (Immagine per gentile concessione di Analog Devices)

I progetti a frequenza di taglio variabile possono essere implementati anche con filtri a condensatore commutati. LTC1068-25IG#PBF di Analog Devices è un filtro passa-basso universale a condensatore commutato dell'8° ordine con una frequenza di taglio massima di 200 kHz. Questo CI è costituito da quattro filtri del 2° ordine che possono essere collegati in cascata per creare un filtro passa-basso dell'8° ordine (Figura 8).

Figura 8: Filtro passa-basso dell'8° ordine utilizzando un filtro a condensatore commutato LTC1068-25IG#PBF. La frequenza di taglio è impostata utilizzando il clock di commutazione ed è uguale alla frequenza di clock di commutazione divisa per 32. (Immagine per gentile concessione di Analog Devices)

I circuiti integrati dei filtri attivi universali possono essere utilizzati anche per l'antialiasing. Richiedono un numero maggiore di componenti per impostare le caratteristiche del filtro. LTC1562-2 di Analog Devices è un filtro quadruplo a basso rumore/bassa distorsione del 2° ordine che può essere configurato come un filtro Butterworth, Chebyshev, ellittico o a risposta con ritardo equiripple con risposta passa-basso, passa-alto o passa banda. Le frequenze di taglio vanno da 20 a 300 kHz utilizzando la programmazione del valore del resistore. Tre resistori programmano la frequenza centrale, il guadagno e Q. Questo progetto di filtri quadrupli del 2° ordine può essere configurato per produrre filtri del 2°, 4°, 6° o 8° ordine.

Conclusione

Per i sistemi di acquisizione dati sono necessari filtri passa-basso antialiasing per garantire che tutti i segnali di interesse campionati possano essere ricostruiti con precisione. Le caratteristiche del filtro richieste corrispondono alla larghezza di banda, alla risoluzione dell'ampiezza e alla frequenza di campionamento dell'ADC con cui è accoppiato. Come è stato dimostrato, esistono diverse opzioni di progettazione per l'implementazione del filtro passa-basso, compresi i dispositivi attivi, controllabili digitalmente e i condensatori commutati.