Einführung in die Signalverarbeitung: Gleitendes Mittelwertfilter

Signale und Systeme sind mächtige Konzepte in der Elektrotechnik. Sie ermöglichen es uns zu modellieren, wie Informationen elektrische Komponenten passieren und wie sie verändert werden können. Haben wir erst einmal verstanden, wie Signale wie Spannungen durch verschiedene elektrische Komponenten beeinflusst werden, können wir darüber hinaus Schaltungen entwerfen, mit denen wir Signale nach Belieben manipulieren können. Es ist daher faszinierend, wie sich eine Kombination von elektrischen Bauteilen wie Widerständen, Kondensatoren und Operationsverstärkern (OVs) zur Modellierung mathematischer Werkzeuge wie Integration und Differenzierung nutzen lässt.

Schauen Sie sich zum Beispiel die folgende Schaltung an (Abbildung 1):

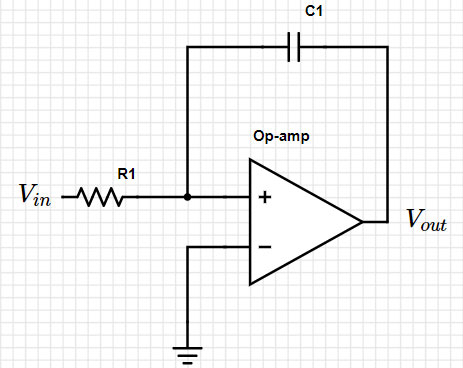Abbildung 1: Einfache Integratorschaltung. (Bildquelle: Mustahsin Zarif)

Durch Laplace-Transformation können wir die Schaltung mit der folgenden Formel darstellen:

Vout = -(1/s) (1/RC) Vin

1/s entspricht im Laplace-Bereich eigentlich der Integration. Wir haben also ein Schaltungsmodell für eine Integratorschaltung mit einem Operationsverstärker. In der Realität sind Systeme jedoch immer mit irgendeiner Form von zufälligem Rauschen kontaminiert.

Betrachten wir uns anstelle der Integratorschaltung ein einfacheres Beispiel, zum Beispiel eine Spannungsverstärkerschaltung, deren Ein- und Ausgangswellenformen mit einem Oszilloskop gemessen werden können (siehe Abbildung 2).

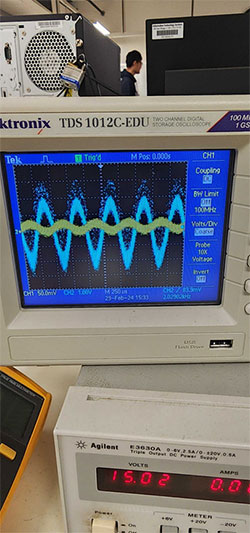Abbildung 2: Ein- und Ausgangswellenformen eines Spannungsverstärkers. (Bildquelle: Mustahsin Zarif)

Das zufällige Rauschen, das zur zugrundeliegenden, sichtbaren Sinuswellenformen hinzukommt, kann auf eine Vielzahl von Faktoren zurückzuführen sein, wie z. B. mangelhafte elektrische Verbindungen, da die Schaltung auf einem Breadboard aufgebaut ist. Dieses Rauschen beeinträchtigt auch die Wellenform des Integrators, was wir in einem zukünftigen Blog in dieser Serie über Signalverarbeitung betrachten werden. Was uns oft interessiert, ist, wie wir die zufälligen Störungen minimieren können.

Filtertechniken

Häufig werden zur Minderung von Störungen Filtertechniken genutzt, die entweder als 1) FIR-Filter (Finite Impulse Response - endliche Impulsantwort) oder 2) IIR-Filter (Infinite Impulse Response - unendliche Impulsantwort) klassifiziert werden können.

FIR-Filter werden so genannt, weil der Ausgang zu jedem Zeitpunkt nur von den aktuellen und vorherigen Eingangswerten abhängt und nicht von den vergangenen Ausgangswerten. Daher weisen sie eine nicht-rekursive Struktur ohne Rückkopplung auf, die in Gleichung 1 modelliert werden kann.

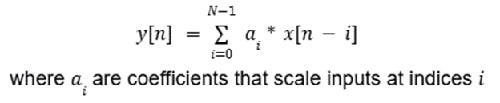Gleichung 1: FIR-Filter-Beispielgleichung. (Bildquelle: Mustahsin Zarif)

Die Integratorschaltung ist ein Beispiel für ein FIR-Filter, da der Ausgang nur vom Eingang abhängig ist.

IIR-Filter hingegen verfügen über eine Rückkopplung, da der Ausgang zu jedem Zeitpunkt sowohl von früheren Ausgängen als auch vom aktuellen Eingang abhängt. Das wird in Gleichung 2 modelliert.

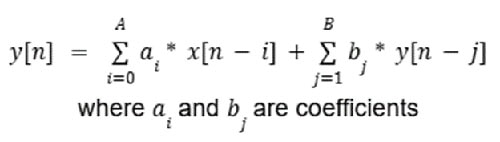Gleichung 2: IIR-Filter-Beispielgleichung. (Bildquelle: Mustahsin Zarif)

Abbildung 3 ist die Blockdiagramm-Darstellung eines IIR-Filters, die zeigt, wie Ein- und Ausgänge verzögert (z-i, z-j), skaliert (ai, bj) und summiert werden, um den aktuellen Ausgang zu erhalten. Indem wir diese Werte ändern, können wir verschiedene Arten von Filtern implementieren.

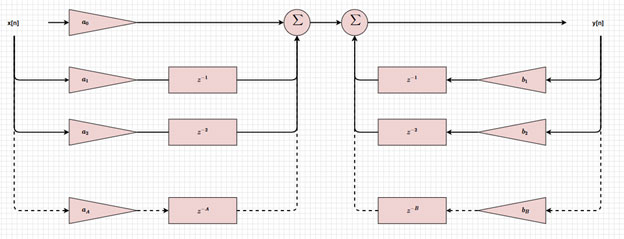Abbildung 3: Blockdiagramm eines IIR-Filters. (Bildquelle: Mustahsin Zarif)

Bei einem Blockdiagramm eines FIR-Filters ohne Rückkopplung wäre y[n] einfach das Ergebnis der ersten Summbildung (Abbildung 4).

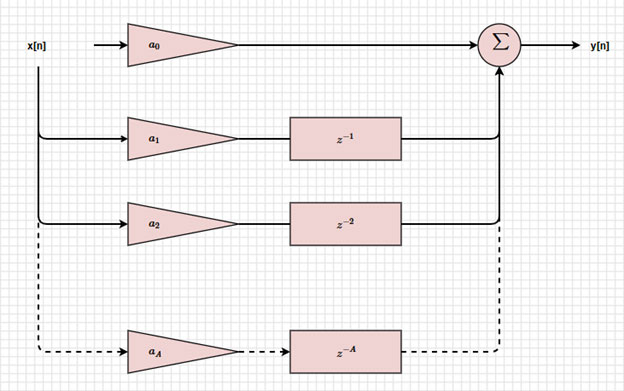Abbildung 4: Blockdiagramm eines FIR-Filters. (Bildquelle: Mustahsin Zarif)

Nachdem wir nun die Grundlagen von FIR- und IIR-Filtern kennen, betrachten wir das Gelernte an einem Beispiel: dem gleitenden Mittelwertfilter.

Beim gleitenden Mittelwert wird der Mittelwert des aktuellen Eingangswerts und einer bestimmten Anzahl vorheriger Eingangswerte gebildet (Gleichung 3).

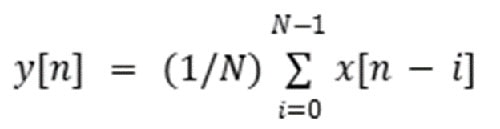Gleichung 3: Gleichung für gleitenden Mittelwert. (Bildquelle: Mustahsin Zarif)

Hierbei ist N die Fenstergröße/Anzahl der Stichproben, die in den Ausgangswert einbezogen werden.

Wir sehen, dass es sich um einen FIR-Filter handelt, da es auf der rechten Seite der Gleichung keine y-Terme gibt.

Wir können die Gleichung jedoch so umstellen, dass ein IIR-Filter entsteht. Nehmen wir Folgendes an:

N=5, also ist

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5

und y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

Daher hängt der aktuelle Ausgangswert jetzt vom vorherigen Ausgangswert ab (y[6] hängt von y[5] ab).

Allgemeiner ausgedrückt:

y[n] = (y[n - 1] + x[n] - x[n - N - 1])/N

Hierbei ist N = Fenstergröße.

Dieses Filter wirkt Wunder bei der Glättung von Signalen im Zeitbereich, wie Abbildung 5 zeigt, die ich mit Python für eine Fenstergröße N = 11 simuliert habe.

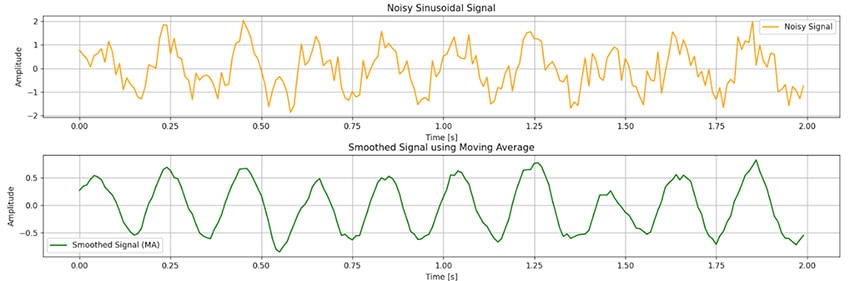Abbildung 5: Simulation eines gleitenden Filters mit Python. (Bildquelle: Mustahsin Zarif)

Python-Code für die Simulation eines gleitenden Filters:

Copyimport numpy as np

import matplotlib.pyplot as plt



# Parameters for the sinusoidal wave

frequency = 5  # in Hertz

sampling_rate = 100  # Sampling rate in samples per second

duration = 2  # in seconds



# Generate time axis

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# Generate a clean sinusoidal signal

clean_signal = np.sin(2  np.pi  frequency * t)



# Add random, white (Gaussian) noise to the signal

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

    window = np.ones(window_size) / window_size

    return np.convolve(signal, window, mode='same') 



# Apply moving average to the noisy signal

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# Plot the noisy and smoothed signals

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

Fazit

Zu Beginn dieses Blogs haben wir gezeigt, wie Daten in der Realität durch Rauschen verfälscht werden. Auch wenn wir nicht die ideale Antwort erhalten, die wir aufgrund mathematischer Gleichungen erwarten würden, ist es dennoch möglich, unerwünschte Eigenschaften aus unseren erfassten Daten herauszufiltern, um der idealen Antwort so nahe wie möglich zu kommen. Hierfür gibt es verschiedene Verfahren ebenso wie verschiedene Situationen, in denen wir diese anwenden können. Dieser Blog schloss mit einer simulierten Reaktion eines gleitenden Mittelwertfilters. Im nächsten Blog werden wir uns ansehen, wie das exponenziell gleitende Mittelwertfilter verrauschte Daten einer Trägheitsmesseinheit glätten kann.