Das Smith-Diagramm: Seine Geschichte und warum es für HF-Designer so wichtig ist

Neulinge im HF-Design, die versuchen, eine direkte Verbindung zwischen zwei Komponenten herzustellen, z. B. von einem spannungsgesteuerten Oszillator (VCO) zu einem Mischer, sind zweifellos schon auf seltsame, kreisförmige Diagramme in den Datenblättern der Komponenten gestoßen, wie z. B. diese für den MAX2472 von Maxim Integrated, einen VCO-Pufferverstärker für 500 bis 2500 Megahertz (MHz) (Abbildung 1). Diese Diagramme, die so genannten Smith-Diagramme, unterscheiden sich deutlich von den Diagrammen aus dem Algebra- oder Statistikunterricht, daran besteht kein Zweifel.

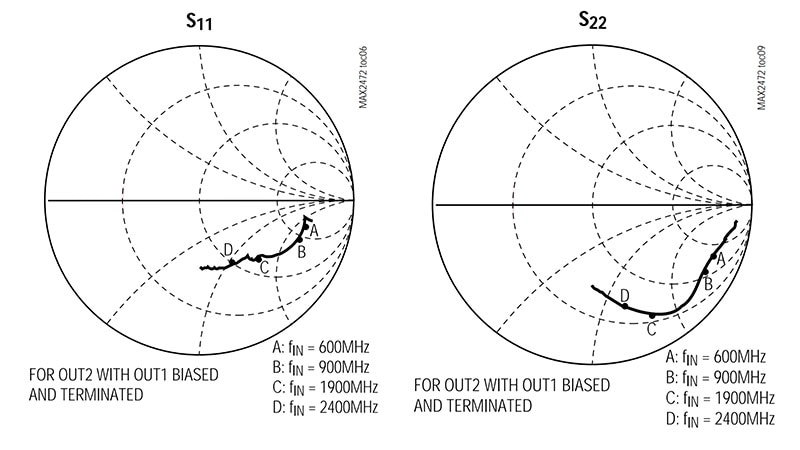Abbildung 1: Viele Datenblätter von HF-Komponenten enthalten Smith-Diagramme, die die Werte von Schlüsselparametern bei verschiedenen Betriebsfrequenzen zeigen, wie z. B. diese für den VCO-Pufferverstärker MAX2472 von Maxim bei 600, 900, 1900 und 2400 MHz. (Bildquelle: Maxim Integrated)

Das Diagramm ist nach Phillip Smith benannt, einem Ingenieur der Bell Telephone Laboratories, der es zwischen 1936 und 1939 entwickelte und verfeinerte, als er sich mit dem Verständnis von Übertragungsleitungen und stehenden Wellen bei den damals so genannten „hohen Frequenzen“ von bis zu 1 MHz (damals Megazyklen pro Sekunde genannt) beschäftigte. Sein seltsam anmutendes Kreisdiagramm ist auch im Zeitalter leistungsfähiger Computer und computergestützter Entwurfswerkzeuge (CAD) zum nützlichsten und leistungsfähigsten Werkzeug für die Arbeit mit und die Optimierung von Hochfrequenzschaltungen im Hinblick auf ihre Eingangs- und Ausgangsimpedanz geworden.

Das Smith-Diagramm bietet unter anderem eine effiziente Möglichkeit zur Visualisierung von Entwurfsoptionen, wenn es darum geht, die Impedanzen von Quelle und Last zwischen den Stufen abzustimmen, was bei vielen Schaltungen, insbesondere bei der HF-Entwicklung, von großer Bedeutung ist. Es gibt zwei Gründe, warum ein solcher Abgleich wichtig ist:

• Erstens muss die komplexe Impedanz R_S + jX_S der Quelle gleich der konjugierten komplexen Impedanz R_L - jX_L der Last sein, um eine maximale Leistungsübertragung von einer Quelle zu einer Last zu erreichen:

Dabei ist R der ohmsche (reale) Teil der Impedanz und X der reaktive (induktive oder kapazitive) Teil (Abbildung 2).

Abbildung 2: Eine große Herausforderung bei der Entwicklung von Hochfrequenz- und Übertragungsleitungen besteht darin, sicherzustellen, dass die Quelle eine Lastimpedanz „sieht“, die die konjugierte komplexe Impedanz der Quelle ist, selbst wenn diese Lastimpedanz nicht vorhanden ist. (Bildquelle: HandsOnRF.com)

• Zweitens: Selbst wenn ein solcher Leistungsverlust kein Problem darstellt (was selten der Fall ist), ist eine Impedanzanpassung erforderlich, um die Reflexion der Energie von der Last zurück zur Quelle zu minimieren, die die Ausgangsschaltung der Quelle beschädigen kann.

Was das Smith-Diagramm zeigt

Das Smith-Diagramm ist eine polare Darstellung des komplexen Reflexionskoeffizienten (auch Gamma genannt und durch rho (Γ) symbolisiert). Es gelingt, was auf den ersten Blick fast unmöglich erscheint: die gleichzeitige grafische Darstellung des Real- und Imaginärteils einer komplexen Impedanz, wobei der Realteil R von 0 bis unendlich (∞) und der Imaginärteil X von minus unendlich bis plus unendlich reichen kann - und das alles auf einem einzigen Blatt Papier.

Ein vereinfachtes Smith-Diagramm, das Kreise mit konstantem Widerstand und Bögen mit konstantem Blindwiderstand zeigt, ist ein guter Ausgangspunkt für das Verständnis seiner Anordnung (Abbildung 3). Als zusätzlicher Vorteil bietet das Diagramm auch eine Möglichkeit, Streuparameter (S-Parameter) zu zeigen und wie ihre Werte mit tatsächlichen Hardware-Messungen und Überlegungen zusammenhängen.

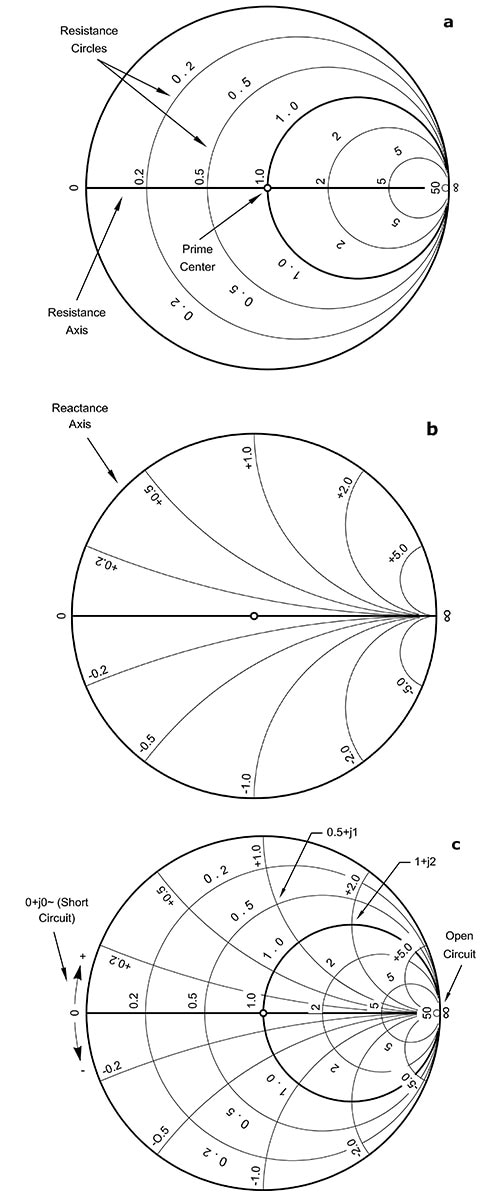Abbildung 3: Das Smith-Diagramm zeigt Bögen mit konstantem Widerstand (a) und Kreise mit konstantem Blindwiderstand (b), die zusammengeführt und überlagert werden (c), um einen Überblick über alle Impedanzmöglichkeiten zu geben. (Bildquelle: ARRL.org)

Sobald diese komplexen Impedanzwerte im Smith-Diagramm markiert sind, kann das Diagramm verwendet werden, um viele Parameter zu identifizieren, die für das Verständnis des HF-Signalpfads oder der Übertragungsleitungssituation entscheidend sind, einschließlich:

• Komplexe Spannungs- und Stromreflexionskoeffizienten.
• Komplexe Spannungs- und Stromübertragungskoeffizienten.
• Reflexions- und Transmissionskoeffizienten der Leistung.
• Reflexionsverlust.
• Rückflussdämpfung.
• Stehwellen-Verlustfaktor.
• Maximale und minimale Spannung und Stromstärke sowie das Stehwellenverhältnis (SWR).
• Form, Position und Phasenverteilung zusammen mit der stehenden Welle von Spannung und Strom.

Aber das ist nur ein Teil der Stärke des Smith-Diagramms. Obwohl es für Entwickler nützlich und oft auch notwendig ist, die oben genannten Parameter zu kennen, kann das Smith-Diagramm auch bei der Analyse und bei Konstruktionsentscheidungen helfen:

• Anzeige der komplexen Impedanzen in Abhängigkeit von der Frequenz.
• Anzeige der s-Parameter eines Netzes in Abhängigkeit von der Frequenz.
• Bewertung der Eingangsreaktanz oder -suszeptanz von offenen und kurzgeschlossenen Stichleitungen.
• Bewertung der Auswirkungen von Nebenschluss- und Reihenimpedanzen auf die Impedanz einer Übertragungsleitung.
• Zur Darstellung und Bewertung der Eingangsimpedanzcharakteristik von resonanten und antiresonanten Stichleitungen, einschließlich der Bandbreite und Q.
• Entwurf von Impedanzanpassungsnetzwerken unter Verwendung einzelner oder mehrerer offener oder kurzgeschlossener Stichleitungen, Viertelwellenleiterabschnitte und L-C-Komponenten.

Die Vorteile des Smith-Diagramms

Auf den ersten Blick mag das vollständig detaillierte Smith-Diagramm wie ein nahezu unverständliches Durcheinander von Linien in alle Richtungen aussehen (Abbildung 4), aber in Wirklichkeit handelt es sich nur um eine höher aufgelöste, detailliertere Darstellung des zuvor gezeigten vereinfachten Diagramms. Sie können eine druckbare Version eines Smith-Diagramms aus den Ressourcen des Online-Innovationshandbuchs von DigiKey herunterladen.

Abbildung 4: Ein typisches Smith-Diagramm kann imposant aussehen, aber es ist nur eine höher aufgelöste, detailliertere Darstellung des zuvor gezeigten vereinfachten Diagramms. (Bildquelle: DigiKey)

Das Smith-Diagramm zeigt mehr als nur eine einzige Lösung für viele designbezogene Probleme: es zeigt die vielen möglichen Lösungen. Der Entwickler kann dann entscheiden, welche von ihnen für die jeweilige Situation geeignete Bauteilwerte bieten, z. B. praktische Werte für Impedanzanpassungsdrosseln und Kondensatoren. In den meisten Fällen sind die Zahlenskalen des Diagramms auf Systeme für 50 Ohm (Ω) „normalisiert“, da dies die am häufigsten verwendete Impedanz im HF-Design ist.

Das Smith-Diagramm ist so wichtig und nützlich, dass viele Prüfgeräte für HF- und Mikrowellenanwendungen, wie z. B. Vektornetzwerkanalysatoren (VNAs), es aufzeichnen und anzeigen können. Der Netzwerkanalysator T3VNA von Teledyne LeCroy bietet beispielsweise einen solchen Modus (Abbildung 5).

Bild 5: Der Vektor-Netzwerkanalysator T3VNA kann die erfassten Daten im Smith-Diagrammformat anzeigen. (Bildquelle: Teledyne LeCroy)

Wie schwer ist es, die Verwendung der Smith-Diagramme zu erlernen? Wie bei den meisten derartigen Fragen ist es dasselbe, als würde man verschiedene Studenten fragen, wie sie die Schwierigkeiten der Infinitesimalrechnung oder der elektromagnetischen Feldtheorie einschätzen: Es kommt darauf an. Es gibt viele Online-Text- und -Video-Tutorials, die mit den Grundlagen des Smith-Diagramms beginnen und dann Gleichungen für Übertragungsleitungen und analytische Perspektiven hinzufügen. Sie gehen auch auf zahlreiche Beispiele für die Verwendung ein. Natürlich gibt es auch Anwendungen und Programme, die das Erstellen von Diagrammen, die Formulierung des Problems und die Bewertung von Optionen mithilfe des Smith-Diagramms erleichtern. Es ist jedoch hilfreich, zunächst die Grundlagen des Diagramms zu verstehen, bevor man auf diese zurückgreift.

Fazit

Es ist erstaunlich, dass ein grafisches Tool, das vor über 80 Jahren entwickelt wurde, lange bevor es das HF-Design, wie wir es heute kennen, überhaupt gab, immer noch eine der wichtigsten Ressourcen für papier- und softwarebasierte HF-Design-Herausforderungen ist. In jedem Fall ist das Smith-Diagramm ein leistungsfähiges Werkzeug zur Darstellung und Bewertung von HF-Parametern und zur Gewinnung von Erkenntnissen über Entwurfsalternativen und die damit verbundenen Kompromisse. Der beste Weg, die Leistungsfähigkeit des Smith-Diagramms und seine Vorteile kennen zu lernen, ist, es zu benutzen und einige der vielen veröffentlichten Beispiele durchzuarbeiten.

Empfohlene Lektüre

1 - „Das Smith-Diagramm: Ein 'altes' grafisches Werkzeug, das im HF-Design immer noch wichtig ist“

https://www.digikey.de/de/articles/the-smith-chart-an-ancient-graphical-tool-still-vital-in-rf-design

2 - „SAW-Filter retten Wireless-Produkte vor unpraktischen diskreten Implementierungen“

https://www.digikey.de/de/articles/saw-filters-rescue-wireless-products-from-impractical-discrete-implementations

3 - „Verständnis der Grundlagen rauscharmer und Leistungsverstärker in Wireless-Designs“

https://www.digikey.de/de/articles/understanding-the-basics-of-low-noise-and-power-amplifiers-in-wireless-designs

4 - „Verwendung von Log-Verstärkern zur Verbesserung der Empfindlichkeit und Leistung in HF- und optischen Verbindungen mit großem dynamischen Bereich“

https://www.digikey.de/de/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers