Warum und wie man digitale Filter für hochauflösende, schnelle Analog/Digital-Wandlungen verwendet

Es ist immer noch eine analoge Welt, und doch ist die digitale Elektronik allgegenwärtig, und das aus gutem Grund. Auch wenn die Digitalisierung viele Probleme mit algorithmischen Ansätzen löst, haben selbst die besten digitalen Algorithmen Unzulänglichkeiten im Umgang mit realen Entitäten, die im analogen Bereich existieren. Dies gilt insbesondere für Anwendungen, die eine schnelle und hochauflösende Datenerfassung erfordern, wie z. B. Instrumentierung, Motorsteuerung und Datenerfassungssysteme.

Das Problem für Entwickler, die solche realen Signale erfassen und verarbeiten wollen, ist die Notwendigkeit, so schnell wie möglich in den digitalen Bereich zu gelangen, ohne die Signalinformationen zu beeinträchtigen. Die Lösung besteht aus einem einfachen Mittelungsalgorithmus (zur Rauschreduzierung) mit einem analogen Tiefpassfilter (LPF) am Frontend. Mit diesen Techniken kann eine geeignete Komponente eine hochauflösende, schnelle Wandlung mit integrierter analoger und digitaler Filterung bieten.

In diesem Artikel werden kurz die Probleme erörtert, die mit dem Erreichen von hochauflösenden Highspeed-Umwandlungen mit einem Analog/Digital-Wandler (ADC) mit sukzessivem Näherungsregister (SAR) unter Verwendung eines analogen LPF und eines digitalen Filters mit Mittelwertbildung verbunden sind, und warum diese Filterkombination für die meisten Anwendungen eine gute Option ist. Anschließend wird der achtkanalige SAR-ADC AD7606C-18 von Analog Devices vorgestellt und gezeigt, wie man die Vorteile seiner Wandlungsrate von 1 Megasample/s (MS/s), seines Konverter-Arrays für simultane Abtastung und seiner flexiblen digitalen Filterfunktionen nutzen kann.

Um zu zeigen, wie die beste Gesamtleistung erreicht werden kann, kombiniert dieser Artikel den AD7606C-18 mit der ebenfalls von Analog Devices stammenden rauscharmen, hochgenauen Spannungsreferenz ADR4525, um die erforderliche SAR-Genauigkeit für 18-Bit-Wandlungen zu verbessern.

Analoge versus digitale Filter

Wenn ein analoger Ingenieur und ein digitaler Ingenieur über Filter diskutieren, kann es sein, dass der digitale Ingenieur den analogen Filter nicht berücksichtigt. Dies wäre ein Fehler. Der Filterungsstandard bei jeder Analog/Digital-Wandlung (A/D) ist, dass der analoge LPF vor dem digitalen Filter liegt (Abbildung 1).

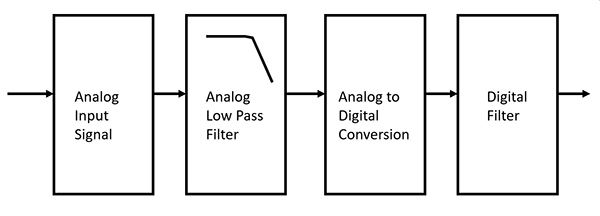Abbildung 1: Ein Blockdiagramm einer Analog/Digital-Signalkette mit dem analogen Filter vor dem digitalen Filter. (Bildquelle: DigiKey)

Nachdem der analoge LPF höhere Frequenzen oberhalb der interessierenden Bandbreite abgeschwächt hat, wandelt der ADC das Signal in ein digitales Wort um. Danach kann der digitale Filter auf das Signal innerhalb der gewünschten Bandbreite wirken.

Analoge Filter in Datenerfassungsumgebungen

Die Bedeutung des analogen LPFs zeigt sich am Ausgang des ADCs. Jedes Signal, das den ADC durchläuft, hat einen Betrag und eine Frequenz, die mit ihm verbunden sind. Am Ausgang des ADCs bleibt der Betrag des Signals zuverlässig gleich, wenn die Signalfrequenz unterhalb der Eingangsbandbreite des ADCs liegt. Obwohl die A/D-Wandlung die Signalgröße bewahrt, gilt dies nicht für die Frequenzen des Signals. Man kann eine Änderung der Frequenzen oberhalb von ½ der Abtastfrequenz des ADCs, f_S, auch bekannt als Nyquist-Abtastrate, beobachten (Abbildung 2).

Abbildung 2: In Grafik (A) hat die Fast-Fourier-Transformation (FFT) eines Eingangssignals fünf Frequenzkomponenten. Nach einer A/D-Wandlung zeigt die FFT-Darstellung in Grafik (B) alle fünf Signale, die unterhalb der halben Abtastfrequenz (f_S) des ADCs auftreten. (Bildquelle: DigiKey)

In Abbildung 2 verwenden beide FFT-Diagramme eine logarithmische Frequenz auf der x-Achse und eine lineare Spannung oder einen Betrag auf der y-Achse. In Grafik (A) zeigt die FFT-Darstellung des analogen Signals das Eingangssignal eines ADCs mit mehreren Signalen oder Rauschen oberhalb der halben ADC-Abtastfrequenz, oder f_S/2.

Beim Vergleich dieser beiden Diagramme ist es hilfreich, die fünf FFT-Signale zu verfolgen. Nach einer ADC-Wandlung bleiben die Beträge des ursprünglichen Signals gleich, aber die Frequenzen oberhalb der halben Abtastfrequenz in (A) werden in (B) wieder unter f_S/2 „gespiegelt“. Dieses Phänomen wird als Signal-Aliasing bezeichnet. Um das Signal genau zu erfassen, muss die Abtastrate f_S des ADCs größer sein als das Zweifache von f_MAX, wobei f_MAX gleich der nutzbaren Bandbreite des Signals ist, gemäß dem Shannon-Nyquist-Abtasttheorem.

Man kann sehen, wie ADCs permanent unerwünschtes Rauschen und unerwünschte Signale in das digitale Ausgangssignal implantieren. Diese Änderung macht es unmöglich, den Unterschied zwischen bandinternen Signalen und bandexternen Signalen am Ausgang des Wandlers zu erkennen.

Man könnte erwarten, dass es einen Weg hin und her zwischen diesen beiden FFT-Darstellungen gibt. Wenn diese Transformation einmal stattgefunden hat, gibt es jedoch kein Zurück und kein Rückgängigmachen. Leider unterstützt die Mathematik diese Art des Hin- und Herwechselns nicht.

Zurück zur Analog/Digital-Debatte: Ein digitaler Filter ist zweifellos in der Lage, eine Mittelwertbildung, eine Filterung mit endlicher Impulsantwort (FIR) oder unendlicher Impulsantwort (IIR) anzuwenden und damit das Systemrauschen zu reduzieren. Jeder digitale Filter erfordert jedoch eine erhebliche Überabtastung (der Prozess der Abtastung eines Signals mit einer Abtastfrequenz, die deutlich höher ist als die endgültige Ausgangsdatenrate), was Zeit und Strom verbraucht und die Abtastgeschwindigkeit des ADCs reduziert. Die digitale Filter- und Wandlerfunktion überwindet das Phänomen der Aliasing-Signale nicht. Am besten ist es, einfach das höherfrequente Rauschen von Anfang an zu reduzieren - selbst mit einem rudimentären analogen LPF erster Ordnung.

Mittelwertbildende digitale Filter

SAR-ADCs verbessern ihre DC-Rauschmessung mit einem mittelwertbildenden digitalen Filter. Der mittelwertbildende digitale Filter erfasst mehrere Umwandlungen mit einer einheitlichen Zeitskala, um die Anzahl der Bits zu erhöhen. ADC-Anwender verwenden Mittelungsalgorithmen mit ihrem Controller, Prozessor oder einer On-Chip-Mittelungs-Engine, die mehrere Wandlerabtastwerte erfasst. Die Mittelwertbildung „glättet“ die Wandlergruppe und verbessert die effektive Auflösung durch Unterdrückung des Systemrauschens.

Die Implementierung der konvertierten Datenglättung beinhaltet mehrere Signalerfassungen mit einer konstanten Abtastrate und Mittelwertbildung über eine vorgegebene Anzahl an Abtastungen. Der Vorgang der Mittelwertbildung ist hinlänglich bekannt. Die Summierung der ADC-Ergebnisse (aufeinanderfolgende Abtastungen, x) geteilt durch die Anzahl der Abtastungen (N) ergibt einen Mittelwert (Gleichung 1).

 Gleichung 1

Dieses Verfahren reduziert die Ausgangsdatenrate um den Faktor N, erhöht aber die Einschwingzeit des Systems.

Die Standardabweichung der gemittelten verrauschten Abtastwerte (σ_avg) ist die Standardabweichung des Originalsignals (σ_sig) geteilt durch die Quadratwurzel aus N (Gleichung 2).

 Gleichung 2

Die aufeinanderfolgenden Abtastungen, einschließlich des unkorrelierten Rauschens, führen zu einer stärkeren Rauschunterdrückung bei einem konstanten Signalmittelwert. Jede aufeinanderfolgende gemittelte Abtastung führt zu einer Verbesserung des Signal-Rausch-Verhältnisses (SNR), wenn das Signal DC ist und die Rauschkomponente zufällig ist.

Die SNR-Verbesserung ist proportional zur Quadratwurzel aus der Anzahl der gemittelten Samples. Ein Mittelwert von vier DC-Signalabtastungen (4¹) erhöht die effektive Auflösung des Wandlers um eins bei einer Erhöhung des SNR um 6 Dezibel (dB). Ein Mittelwert von 16 bzw. 4² Abtastungen erhöht die effektive Auflösung um zwei und den SNR um 12 dB. Mit dieser Logik erhöht eine Gruppengröße von 4^N die Anzahl der effektiven Bits einer Wandlung um N, wodurch das Systemrauschen auf Null und der SNR-Wert auf unendlich gebracht wird.

Die Allan-Varianz

Ein SNR-Wert, der gleich unendlich ist, ist natürlich absurd. In der realen Welt dauert die Erfassung der benötigten Anzahl von Abtastungen Zeit, während der sich das System in Form von Driftgraden verändern kann.

Die Allan-Varianz, auch bekannt als Zwei-Abtastwert-Varianz, misst die Frequenzstabilität in Uhren, Oszillatoren, ADCs und Verstärkern, indem sie die Änderung des Rauschens zeigt, wenn die Anzahl der bei der Mittelung eines Signals verwendeten Abtastwerte erhöht wird. Das statistische Analysewerkzeug Allan-Varianz bestimmt die maximale Anzahl der erforderlichen Stichproben, die für ein bestimmtes System optimal ist, und schätzt so die Stabilität durch Aufzeigen von Frequenzdrift oder Temperatureffekten.

Beispielsweise können die Daten in einem System von einem ADC im Laufe der Zeit Verschiebungen aufweisen, wie in Abbildung 3 dargestellt.

Abbildung 3: Die 30.000 ADC-Ausgangsdatenpunkte, die über einen Zeitraum von neun Minuten erfasst wurden, zeigen eine leichte Drift in den Daten über diesen Zeitraum, was zu einer Verschlechterung der Berechnung der Allan-Varianz führt. (Bildquelle: Electronic Design)

Der Varianzalgorithmus nimmt mehrere Stapel von immer längeren Mittelwerten und bewertet das resultierende Rauschen jedes Stapels (Abbildung 4).

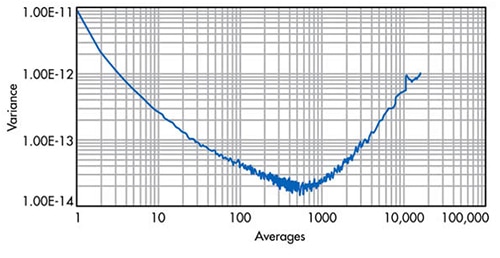Abbildung 4: Angewandte Allan-Varianzberechnung für die Datenpunkte in Abbildung 3. Bei einem Mittelwert von 500 Punkten erreicht dieses spezielle ADC-System 4,48 Bit oder eine Steigerung des SNR um 27 dB. (Bildquelle: Electronic Design)

Abbildung 4 zeigt, dass die minimale Varianz der Datenpunkte dieses speziellen Systems bei etwa 500 ADC-Ausgangsmittelwerten auftritt - die optimale Anzahl von Abtastmittelwerten für die Rauschunterdrückung. Bei einem Mittelwert von 500 Punkten erreicht dieses spezielle ADC-System 4,48 Bit oder eine Steigerung des SNR um 27 dB. Vor und nach dem 500. Durchschnittspunkt verschlechtern sich die Ergebnisse in Abbildung 4, da die Datendrift ein größerer Faktor wird. Variablen, die sich auf die Berechnung der Allan-Varianz auswirken, können Zeit, Signalstabilität, Drift, Schwankungen in der Stromversorgung und Produktalterung sein. Wenn ein digitaler Mittelungsfilter verwendet wird, ist es ratsam, das Gesamtsystem mit dem Allan-Varianz-Tool zu bewerten.

Lösung für die reale Welt

SAR-Wandler können programmierbare Verstärker- (PGA) und digitale Filterfunktionen bieten, um die effektive Auflösung und die Spannung des niedrigstwertigen Bits (LSB) zu verbessern. Der AD7606C-18 von Analog Devices zum Beispiel ist ein 18-Bit-A/D-Datenerfassungssystem (DAS) mit 1 MS/s Simultanabtastung und acht Kanälen, von denen jeder einen analogen Eingangs-Klemmschutz, einen PGA, einen LPF und einen 18-Bit-SAR-ADC enthält.

Der Baustein verfügt außerdem über analoge Eingangspuffer mit einer Eingangsimpedanz von 1 Megaohm (MΩ) und programmierbaren Konfigurationen für echte bipolare Differenz-Eingangsspannungen sowie bipolare und unipolare referenzbezogene Eingangsspannungen. Der AD7606C-18 ermöglicht den Anschluss von acht verschiedenen unabhängigen Eingangssensoren oder Signalkanälen.

Der digitale Filter des AD7606C-18 verfügt über einen Überabtast-Modus, der den Mittelwert von sich wiederholenden Abtastungen von 1 bis 256 (4⁴) bildet. Laut dem Allan-Varianz-Tool verbessert diese Überabtastfunktion das Rauschverhalten am digitalen Ausgang des Wandlers. Die rauscharme 2,5-Volt-Präzisionsspannungsreferenz ADR4525 ergänzt das DAS-System AD7606C-18 mit einem maximalen Temperaturkoeffizienten von 1 Teil pro Million pro Grad Celsius (ppm/°C) und einem typischen Ausgangsrauschen von 1 Mikrovolt (µV) Spitze-Spitze (Abbildung 5).

Abbildung 5: Der SAR-ADC AD7606C-18 mit der 2,5-Volt-Präzisionsspannungsreferenz ADR4525. Die Induktivitäten mit LPFs erster Ordnung an den Eingangskanälen V1 bis V8 tasten alle acht Kanäle gleichzeitig ab. (Bildquelle: Analog Devices)

Wie Abbildung 5 zeigt, kann diese Art von SAR-Array mit hoher Eingangsimpedanz direkt mit Sensoren verbunden werden, ohne die typischen externen Treiberverstärker. Eine externe Sensorverstärkungsstufe kann ebenfalls entfallen. Gleichzeitig verfügt der SAR-Wandler über eine interne PGA- und LPF-Stufe, die für die Signalverarbeitung sorgt, gefolgt von einem digitalen Mittelungsfilter, um das Rauschen weiter zu reduzieren und eine höhere effektive Auflösung zu erreichen. Ein solches DAS kann eine effektive Auflösung von 17,1 Bit mit einer Wandlungsgeschwindigkeit von 3,9 Kilosamples pro Sekunde (kS/s) bieten. Am anderen Ende des Spektrums der Wandlungsgeschwindigkeit bietet diese Komponente eine effektive Auflösung von 15 Bit mit einer Wandlungsgeschwindigkeit von 1 MS/s.

Die schnellste Wandlungsgeschwindigkeit des AD7606C-18 beträgt 1 MS/s bei einer Überabtastung von eins. Wenn die Kanal-Überabtastung des Konverters zwei beträgt oder die Abtastungen eines Kanals zweimal gemittelt werden, beträgt die Konvertierungsgeschwindigkeit die Hälfte der maximalen Konvertierungsgeschwindigkeit bei 500 kS/s. Bei einer Überabtastung von vier bzw. 4¹ als Anzahl der gemittelten Abtastungen beträgt die Wandlungsgeschwindigkeit dieses Kanals 250 kS/s usw. Für jeden der acht Kanäle bietet das System mit einem Überabtastwert von 256 einen referenzbezogenen Bereich von ±10 Volt, 17,1 Bit effektive Auflösung (105 dB SNR) und eine Wandlungsgeschwindigkeit von 3,9 kS/s (Tabelle 1).

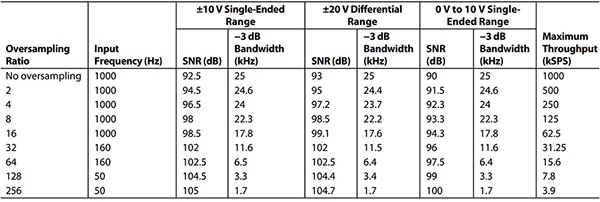Tabelle 1: Überabtastperformance bei niedriger Bandbreite des AD7606C-18. (Bildquelle: Analog Devices)

Die Formel für die Umrechnung von SNR in die effektive Auflösung (effektive Anzahl von Bits oder ENOB) ist in Gleichung 3 dargestellt.

 Gleichung 3

Am anderen Ende des Spektrums der Wandlungsgeschwindigkeit bietet diese Komponente mit einem Überabtastungfaktor von 1 eine effektive Auflösung von 15 Bit (92,5 dB SNR) bei einer Wandlungsgeschwindigkeit von 1 MS/s (Tabelle 1).

Es gibt weitere Verbesserungen, die der AD7606C-18 bietet. Da acht separate SAR-ADCs auf dem Chip vorhanden sind, haben alle acht Kanäle eine simultane Abtastfunktion. Mit dieser Funktion ist es möglich, den digitalen Filter zu implementieren, um eine hohe Auflösung oder eine hohe Geschwindigkeit gleichzeitig auf allen Kanälen zu erreichen. Zusätzlich sind alle Kanäle kalibrier- und diagnosefähig.

Zum Beispiel erkennt die Systemphasenkalibrierung des AD7606C-18 eine Fehlanpassung des diskreten Eingangsfilters. Diese wertvolle Funktion identifiziert jede Fehlanpassung an den diskreten Komponenten oder im verwendeten Sensor, die eine Phasenfehlanpassung zwischen gleichzeitig abgetasteten Kanälen verursachen kann. Der Softwaremodus der Komponente kompensiert die Phasenfehlanpassung auf einer kanalweisen Basis, indem der Abtastzeitpunkt eines einzelnen Kanals verzögert wird.

Die Kalibrierung der Systemverstärkung erfasst die Widerstandsfehlanpassungen des diskreten Eingangsfilters. Diese Fähigkeit hilft, externe Widerstandsfehlanpassungen zu überwinden. Der Softwaremodus kompensiert den Verstärkungsfehler auf einer kanalweisen Basis, indem der verwendete Serienwiderstandswert in das entsprechende Register geschrieben wird.

Die System-Offset-Kalibrierung berücksichtigt die Eingangssignal-Offsets während der Kalibrierungsaktivität. Die Software kann den Offset des externen Sensors jedes Kanals oder den Offset einer Fehlanpassung des externen Widerstandspaars einstellen.

Für eine spezielle Anwendung verfügt das Board EVAL-AD7606SDZ für den AD7606 über eine Software, die bei der Komponentenevaluierung mit der Komponentenprogrammierung sowie der Wellenform-, Histogramm- und FFT-Erfassung hilft (Abbildung 6).

Abbildung 6: Die Evaluierungsplatine AD7606 (links) ist mit der System-Demonstrationsplattform (SDP) verbunden (rechts), die die Steuerung der Evaluierungsplatine über den USB-Anschluss eines PCs ermöglicht. (Bildquelle: Analog Devices)

Die Software des Evaluierungsboards ermöglicht es dem Benutzer, den Überabtastwert, den Eingangsbereich und die Anzahl der Abtastungen für jeden Kanal sowie die Auswahl des aktiven Kanals zu konfigurieren. Zusätzlich ermöglicht diese Software auch das Speichern und Öffnen von Testdaten-Dateien.

Fazit

Trotz der Umstellung auf Digitaltechnik ist unsere Welt immer noch analog, und die Entwickler brauchen analoge Elektronik, um hochauflösende und schnelle Wandlungsprobleme zu lösen. Wie gezeigt, steigert die einfache Kombination aus analogem LPF und digitalem Mittelungsfilter - implementiert mit der entsprechenden Anzahl gemittelter Abtastwerte - die Leistung eines 1 MS/s-SAR-Wandlers erheblich.